题目内容
已知从A地去B地有两条路可走,并且汽车走路①堵车的概率为
;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.
(Ⅰ)若这三辆汽车中恰有一辆汽车被堵的概率为
,求走公路②堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求这三辆汽车中被堵车辆的辆数ξ的分布列和数学期望.
| 1 |
| 4 |
(Ⅰ)若这三辆汽车中恰有一辆汽车被堵的概率为
| 7 |
| 16 |
(Ⅱ)在(Ⅰ)的条件下,求这三辆汽车中被堵车辆的辆数ξ的分布列和数学期望.
分析:(Ⅰ)本题是一个独立重复试验,走公路②堵车的概率为p,不堵车的概率为1-p,根据独立重复试验的概率公式写出关于p的方程,解出p的值,得到结果
(Ⅱ)确定三辆汽车中被堵车辆的个数ξ的可能取值,结合变量对应的事件和相互独立事件同时发生的概率写出变量的分布列,从而可求数学期望.
(Ⅱ)确定三辆汽车中被堵车辆的个数ξ的可能取值,结合变量对应的事件和相互独立事件同时发生的概率写出变量的分布列,从而可求数学期望.
解答:解:(Ⅰ)由已知条件得
•
•
•(1-p)+(
)2p=
,即3p=1,∴p=
…(5分)
(Ⅱ)ξ可能的取值为0,1,2,3
P(ξ=0)=
•
•
=
;P(ξ=1)=
;P(ξ=2)=
•
•
+
•
•
•
=
;P(ξ=3)=
•
•
=
ξ的分布列为:
所以Eξ=0×
+1×
+2×
+3×
=
.…(12分)
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
| 1 |
| 3 |
(Ⅱ)ξ可能的取值为0,1,2,3
P(ξ=0)=
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 48 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 6 |
| 1 |
| 48 |
| 5 |
| 6 |
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发的概率,考查利用概率知识解决实际问题,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 ;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.
;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率; ;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.
;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.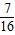 ,求走公路②堵车的概率;
,求走公路②堵车的概率;