题目内容
设O是正△ABC的中心，则向量
，
，
是（ ）
| AO |
| BO |
| CO |
分析：易知O是正△ABC外接圆的圆心，从而|
|=|
|=|
|=R（R为△ABC外接圆的半径），由此可得结论．
| OA |
| OB |
| OC |
解答：解：因为O是正△ABC的中心，
所以|
|=|
|=|
|=R（R为△ABC外接圆的半径），
所以向量
，
，
是模相等的向量，
故选B．
所以|
| OA |
| OB |
| OC |
所以向量
| AO |
| BO |
| CO |
故选B．
点评：本题考查相等向量的定义，属基础题，正确理解相等向量的定义是解决问题的关键．
练习册系列答案
相关题目
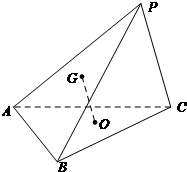如图，在三棱锥P-ABC中，△ABC是正三角形，且∠PCA=∠PCB．
用向量探索几何的性质：
如图，在正四棱锥S-ABCD中，AB=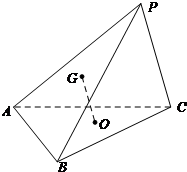
如图，在三棱锥P-ABC中，△ABC是正三角形，且∠PCA=∠PCB．