题目内容
已知幂函数y=f(x)经过点(4,2),则函数y=f(x2-3x-4)的单调递增区间为________.
[4,+∞)
分析:设f(x)=xa,由4a=2,得a= ,从而求得f(x),进而可得函数的定义域,根据复合函数的单调性在定义域内求出y=x2-3x-4的增区间即可.
,从而求得f(x),进而可得函数的定义域,根据复合函数的单调性在定义域内求出y=x2-3x-4的增区间即可.
解答:设f(x)=xa,由题意得,4a=2,解得a= ,
,
所以f(x)=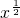 ,则y=f(x2-3x-4)=
,则y=f(x2-3x-4)= ,
,
由x2-3x-4≥0,解得x≥4或x≤-1,
所以y=f(x2-3x-4)的定义域为[4,+∞)∪(-∞,-1].
因为f(x)=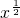 在[0,+∞)上递增,y=x2-3x-4在[4,+∞)上递增,(-∞,-1]上递减,
在[0,+∞)上递增,y=x2-3x-4在[4,+∞)上递增,(-∞,-1]上递减,
所以y=f(x2-3x-4)的单调递增区间为[4,+∞).
故答案为:[4,+∞).
点评:本题考查复合函数的单调性、幂函数的单调性,复合函数单调性的判断方法是:同增异减.
分析:设f(x)=xa,由4a=2,得a=
 ,从而求得f(x),进而可得函数的定义域,根据复合函数的单调性在定义域内求出y=x2-3x-4的增区间即可.
,从而求得f(x),进而可得函数的定义域,根据复合函数的单调性在定义域内求出y=x2-3x-4的增区间即可.解答:设f(x)=xa,由题意得,4a=2,解得a=
 ,
,所以f(x)=
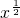 ,则y=f(x2-3x-4)=
,则y=f(x2-3x-4)= ,
,由x2-3x-4≥0,解得x≥4或x≤-1,
所以y=f(x2-3x-4)的定义域为[4,+∞)∪(-∞,-1].
因为f(x)=
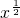 在[0,+∞)上递增,y=x2-3x-4在[4,+∞)上递增,(-∞,-1]上递减,
在[0,+∞)上递增,y=x2-3x-4在[4,+∞)上递增,(-∞,-1]上递减,所以y=f(x2-3x-4)的单调递增区间为[4,+∞).
故答案为:[4,+∞).
点评:本题考查复合函数的单调性、幂函数的单调性,复合函数单调性的判断方法是:同增异减.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目