题目内容
设a为实数,函数f(x)=x|x2﹣a|.
(1)当a=1时,求函数f(x)在区间[﹣1,1]上的最大值和最小值;
(2)求函数f(x)的单调区间.
(1)当a=1时,求函数f(x)在区间[﹣1,1]上的最大值和最小值;
(2)求函数f(x)的单调区间.
解:(1)当a=1时,f(x)=x|x2﹣1|.
∵x∈[﹣1,1],
∴f(x)=﹣x3+x,则f′(x)=﹣3x2+1=﹣3(x﹣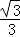 )(x+
)(x+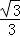 ),
),
令f′(x)=0,得x=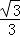 ,x=-
,x=-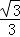 ,
,
∵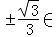 [﹣1,1],
[﹣1,1],
f(﹣1)=1﹣1=0,
f(﹣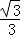 )=﹣(﹣
)=﹣(﹣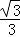 )3﹣
)3﹣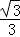 =
=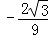 ,
,
f(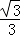 )=
)=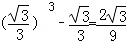 ,
,
f(1)=﹣1+1=0,
∴函数f(x)在x∈[﹣1,1]上的最小值为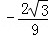 ,最大值为
,最大值为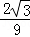 .
.
(2)(i)当a=0时,f(x)=x3,f(x)的单调增区间为(﹣∞,+∞).
(ii)当a<0时,f(x)=x2﹣ax,
∵f′(x)=3x2﹣a>0恒成立,
∴f(x)在(﹣∞,+∞)上单调递增,
∴f(x)的增区间为(﹣∞,+∞).
(iii)当a>0时,①当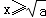 或
或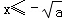 时,f(x)=x3﹣ax,
时,f(x)=x3﹣ax,
因为f′(x)=3x2﹣a=3(x+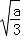 )(x﹣
)(x﹣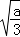 ),﹣
),﹣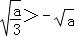 ,
,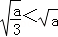 ,
,
所以,当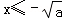 或
或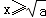 时,f′(x)>0,
时,f′(x)>0,
从而f(x)的单调减区间为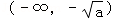 及
及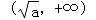 .
.
②当﹣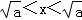 时,f(x)=﹣x3+ax, f′(x)=﹣3x2+a=﹣3
时,f(x)=﹣x3+ax, f′(x)=﹣3x2+a=﹣3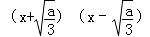 ,
,
令f′(x)=0,得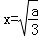 ,x=﹣
,x=﹣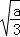 ,列表,得
,列表,得
 综上所述,当a≤0时,函数f(x)的单调增区间为(﹣∞,+∞);
综上所述,当a≤0时,函数f(x)的单调增区间为(﹣∞,+∞);
当a>0时,函数f(x)的单调增区间为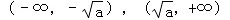 及
及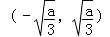 , f(x)的单调减区间为
, f(x)的单调减区间为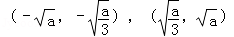 .
.
∵x∈[﹣1,1],
∴f(x)=﹣x3+x,则f′(x)=﹣3x2+1=﹣3(x﹣
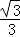 )(x+
)(x+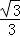 ),
),令f′(x)=0,得x=
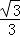 ,x=-
,x=-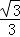 ,
,∵
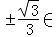 [﹣1,1],
[﹣1,1],f(﹣1)=1﹣1=0,
f(﹣
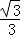 )=﹣(﹣
)=﹣(﹣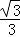 )3﹣
)3﹣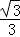 =
=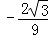 ,
,f(
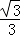 )=
)=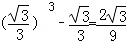 ,
,f(1)=﹣1+1=0,
∴函数f(x)在x∈[﹣1,1]上的最小值为
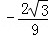 ,最大值为
,最大值为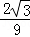 .
.(2)(i)当a=0时,f(x)=x3,f(x)的单调增区间为(﹣∞,+∞).
(ii)当a<0时,f(x)=x2﹣ax,
∵f′(x)=3x2﹣a>0恒成立,
∴f(x)在(﹣∞,+∞)上单调递增,
∴f(x)的增区间为(﹣∞,+∞).
(iii)当a>0时,①当
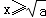 或
或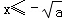 时,f(x)=x3﹣ax,
时,f(x)=x3﹣ax,因为f′(x)=3x2﹣a=3(x+
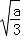 )(x﹣
)(x﹣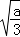 ),﹣
),﹣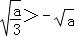 ,
,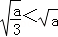 ,
,所以,当
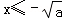 或
或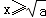 时,f′(x)>0,
时,f′(x)>0,从而f(x)的单调减区间为
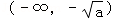 及
及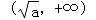 .
.②当﹣
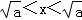 时,f(x)=﹣x3+ax, f′(x)=﹣3x2+a=﹣3
时,f(x)=﹣x3+ax, f′(x)=﹣3x2+a=﹣3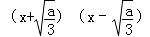 ,
,令f′(x)=0,得
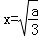 ,x=﹣
,x=﹣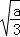 ,列表,得
,列表,得 
当a>0时,函数f(x)的单调增区间为
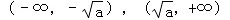 及
及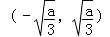 , f(x)的单调减区间为
, f(x)的单调减区间为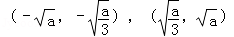 .
. 
练习册系列答案
相关题目