题目内容

20．已知抛物线y2=8x的焦点为F，过F且斜率为2的直线交抛物线于A、B两点．
（1）求|AB|．
（2）求AB的中点M的坐标及|FM|．

分析 （1）先根据抛物线方程求得抛物线的焦点坐标，进而根据点斜式求得直线的方程与抛物线方程联立，消去y，根据韦达定理求得x1+x2的值，进而根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+p得答案；
（2）利用（1），可得AB的中点M的坐标，从而求出|FM|．

解答 解：（1）抛物线焦点为（2，0）
则直线方程为y=2x-4，代入抛物线方程得x2-6x+4=0
∴x1+x2=6
根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+p=6+4=10．
（2）AB的中点M的横坐标为3，纵坐标为2×3-4=2，∴M（3，2），
∴|FM|=$\sqrt{（3-2）^{2}+（2-0）^{2}}$=$\sqrt{5}$

点评 本题主要考查了抛物线的简单性质，考查学生的计算能力．解题的关键是灵活利用了抛物线的定义．

练习册系列答案
相关题目
10．已知函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$，其中$\overrightarrow{m}$=（$\sqrt{3}$，sin2x），$\overrightarrow{n}$=（2cos2x+1，1），x∈R．
（1）求函数f（x）的对称轴方程；
（2）若x1，x2$∈[\frac{π}{12}，\frac{π}{2}]$，x1≠x2，且满足f（x1）+f（x2）=4$\sqrt{3}$，求|x1-x2|的最大值．
11．已知数列{an}和{bn}满足下列关系式：a1=0，b1=2，且$\left\{\begin{array}{l}{{a}_{n+1}=4{a}_{n}+{b}_{n，}}\\{{b}_{n+1}=3{a}_{n}+6{b}_{n}}\end{array}\right.$
（1）设数列{cn}满足cn=bn+λan，证明存在实数λ，使得数列{cn}为等比数列；
（2）求数列{an}和{bn}的通项公式．
8．我们用card（A）来表示有限集合A中元素的个数，例如，A={a，b，c}．则card（A）=3，设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+x，x≤0}\\{lgx，x＞0}\end{array}\right.$，若A={x|f（f（x）=0，x∈R}．则card（A）=（　　）
A．6B．7C．8D．9
15．已知正方形ABCD和矩形ACEF所在的平面互相垂直，$AB=\sqrt{2}$，AF=1，M是线段EF的中点．
（1）求证：AM∥平面BDE；
（2）求证：AM⊥平面BDF．
（3）求直线DE与AM所成角的余弦值．
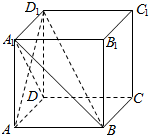5．如图，在正方体ABCD-A1B1C1D1中．
（1）求异面直线A1B与AD1所成的角；
（2）求证：A1D⊥平面ABD1．
12．设数列{xn}的各项都为正数且x1=1．如图，△ABC所在平面上的点Pn（n∈N*）均满足△PnAB与△PnAC的面积比为3：1，若（2xn+1）$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$，则x5的值为31．
9．已知p：$\frac{2x-1}{x+2}$＜1，q：|x-a|＜2．若p是q的必要不充分条件，求实数a的取值范围．
10．已知函数f（x）=alnx+$\frac{1}{2}$ax2+bx（a≠0）．
（I）若函数f（x）的图象在x=1处的切线方程为y=3x-$\frac{3}{2}$b，求a，b的值；
（Ⅱ）若当a=2时，函数f（x）在R上是增函数，求实数b的取值范围；
（Ⅲ）设函数g（x）=1nx的图象C1与函数h（x）=f（x）-ag（x）的图象C2交于点P、Q，过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N，问是否存在点R，使C1在M处的切线与C2在N处的切线平行？若存在，求出R的横坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网