题目内容

17．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，（x≤0）}\\{-{x}^{\frac{1}{2}}，x＞0}\end{array}\right.$．
（1）作出它的图象；
（2）指出函数的单调区间．

分析 （1）由分段函数的图象画法可得f（x）的图象；
（2）由图象观察即可得到所求函数的单调区间．

解答 解：（1）函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，（x≤0）}\\{-{x}^{\frac{1}{2}}，x＞0}\end{array}\right.$的图象如图所示：
（2）结合图象可得f（x）的增区间为（-∞，0），
减区间为（0，+∞）．

点评 本题考查分段函数的图象和运用：求单调区间，考查数形结合的思想方法，属于基础题．

练习册系列答案
相关题目
7．已知数列{an}的前n项和为Sn=n2+1，数列{bn}满足：bn=$\frac{2}{{a}_{n}+1}$，前n项和为Tn．设Cn=T2n+1-Tn．
（1）求数列{bn}的通项公式．
（2）求证：数列{Cn}是单调递减数列；
（3）若对n≥k时．总有Cn＜$\frac{16}{21}$成立．求自然数k的最小值．
8．已知集合M={1，-2，3}，N={-4，5，6，-7}，从两个集合中各取一个元素作为点的坐标，则在直角坐标系中第一，二象限不同点的个数为（　　）
A．18B．14C．16D．10
5．设集合A为函数y=ln（-x2-2x+8）的定义域，集合B为函数y=x+$\frac{1}{x}$-1的值域．集合C为不等式（ax-$\frac{1}{a}$）（x+4）≤0的解集．
（1）求A∩B；
（2）若C⊆CRA，求实数a的取值范围．
12．函数f（x）=|lgx2|为（　　）
A．奇函数，在区间（1，+∞）上是减函数B．奇函数，在区间（1，+∞）上是增函数
C．偶函数，在区间（0，1）上是增函数D．偶函数，在区间（0，1）上是减函数．
2．在命题“m＞0，n＞0，若椭圆mx2+ny2=1的焦点在x轴上，则m＞n”的逆命题、否命题、逆否命题中，真命题个数是（　　）
A．0B．1C．2D．4
9．在△ABC中，角A，B、C的对边分别为a，b，c，且向量$\overrightarrow{m}$=（sin（A-B），a2-b2）与向量$\overrightarrow{n}$=（sin（A+B），a2+b2）共线，若角c=120°，则角A=30°．
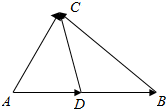6．如图，在△ABC中，∠ACB的平分线CD交AB于D，$\overrightarrow{AC}$的模为2，$\overrightarrow{BC}$的模为3，$\overrightarrow{AD}$的模为1，那么$\overrightarrow{DB}$的模为$\frac{3}{2}$．
7．求下列各三角函数值：
（1）sin3π；
（2）sin18π；
（3）cos5π；
（4）cos25π；
（5）sin$\frac{9π}{2}$；
（6）sin$\frac{13π}{3}$；
（7）cos$\frac{47π}{2}$；
（8）cos$\frac{103π}{4}$；
（9）tan$\frac{37π}{6}$；
（10）tan$\frac{17π}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网