题目内容
设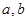 是两条直线,
是两条直线,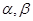 是两个平面,则下列4组条件中:①
是两个平面,则下列4组条件中:①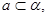
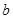 ∥
∥ ,
,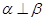 ;②
;②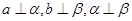 ;③
;③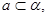
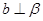 ,
,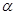 ∥
∥ ;④
;④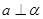 ,
,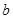 ∥
∥ ,
,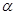 ∥
∥ 。
。
能推得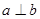 的条件有( )组。
的条件有( )组。
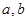 是两条直线,
是两条直线,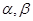 是两个平面,则下列4组条件中:①
是两个平面,则下列4组条件中:①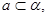
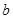 ∥
∥ ,
,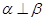 ;②
;②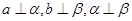 ;③
;③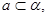
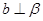 ,
,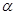 ∥
∥ ;④
;④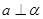 ,
,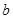 ∥
∥ ,
,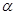 ∥
∥ 。
。能推得
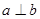 的条件有( )组。
的条件有( )组。A.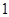 | B.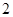 | C.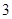 | D.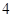 |
C
因为①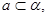
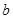 ∥
∥ ,
,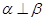 ;则
;则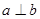 不一定成立
不一定成立
②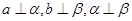 ;显然成立。
;显然成立。
③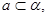
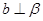 ,
,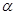 ∥
∥ ;满足线面垂直的性质定理,故成立。
;满足线面垂直的性质定理,故成立。
④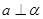 ,
,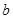 ∥
∥ ,
,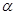 ∥
∥ ,满足线面垂直的性质定理,成立。故选C
,满足线面垂直的性质定理,成立。故选C
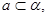
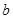 ∥
∥ ,
,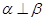 ;则
;则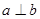 不一定成立
不一定成立②
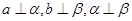 ;显然成立。
;显然成立。③
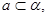
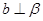 ,
,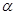 ∥
∥ ;满足线面垂直的性质定理,故成立。
;满足线面垂直的性质定理,故成立。④
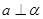 ,
,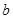 ∥
∥ ,
,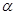 ∥
∥ ,满足线面垂直的性质定理,成立。故选C
,满足线面垂直的性质定理,成立。故选C
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
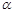 ∩平面
∩平面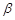 =AB,PQ⊥
=AB,PQ⊥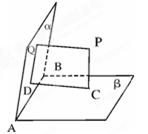
 中,
中, ,
, ,
, .
. ;
;
 的正切值.
的正切值. 
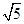 ,点M是PD的中点.
,点M是PD的中点.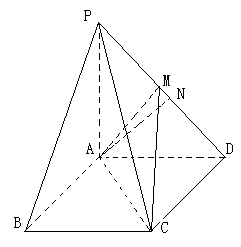
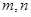 为两条不同的直线,
为两条不同的直线,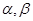 为两个不同的平面,给出下列4个命题:
为两个不同的平面,给出下列4个命题: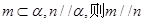 ②若
②若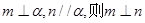
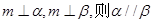 ④若
④若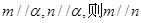
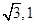
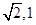
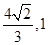

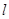 ∥平面
∥平面 ,直线
,直线 ,则
,则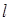 与
与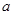 的位置关系是 ( )
的位置关系是 ( )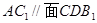 ;
;
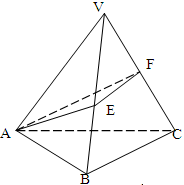
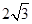 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 ,
的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 ,