题目内容
函数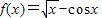
在区间[0，+∞）的零点个数为（ ）A．0
B．1
C．2
D．无穷
【答案】分析：根据余弦函数的最大值为1，可知函数在[π，+∞）上为正值，在此区间上函数没有零点，问题转化为讨论函数在区间[0，π）上的零点的求解，利用导数讨论单调性即可．
解答：解：f′（x）=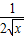
+sinx
①当x∈[0．π）时，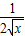
＞0且sinx＞0，故f′（x）＞0
∴函数在[0，π）上为单调增
取x=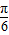
，得f（
）=
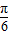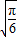-cos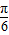
＜0，而f（
）=
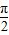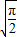＞0，可得函数在区间（0，π）有唯一零点
②当x≥π时，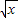
≥
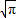＞1且cosx≤1，故函数在区间[π，+∞）上恒为正值，没有零点
综上所述，函数在区间[0，+∞）上有唯一零点
故选B．
点评：本题考查函数的零点，考查分类讨论的数学思想，正确分类是关键．
解答：解：f′（x）=
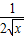+sinx①当x∈[0．π）时，
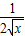＞0且sinx＞0，故f′（x）＞0∴函数在[0，π）上为单调增
取x=
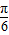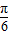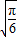，得f（）=-cos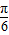＜0，而f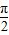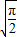（）=＞0，可得函数在区间（0，π）有唯一零点②当x≥π时，
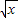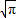≥＞1且cosx≤1，故函数在区间[π，+∞）上恒为正值，没有零点综上所述，函数在区间[0，+∞）上有唯一零点
故选B．
点评：本题考查函数的零点，考查分类讨论的数学思想，正确分类是关键．
练习册系列答案
名校课堂系列答案
相关题目