Question

如图，在棱长为a的正方体ABCD-

A

1

B1C1D1的面ABB₁A₁所在平面内有一点P，满足P到棱

A

1

B1所在直线的距离等于P到棱CC₁所在直线的距离，延长棱B₁B至点E，使得|B1E|=

2

|B1B|，过点E作平行于

A

1

B1的直线l交动点P的轨迹Γ于点M，N，在分别过M，N做轨迹Γ的切线交于点Q，则△MQN的面积为（　　）

• A．

  2

  3

  a2
• B．

  2

  3

  a2
• C．

  3

  2

  a2
• D．

  2

  2

  a2

Answer 1

分析：根据题意求出点P的轨迹为双曲线，在平面ABB₁内运用圆锥曲线知识求出M、N、Q三点的坐标，则三角形MNQ的底边和高可求，从而求出面积．

解答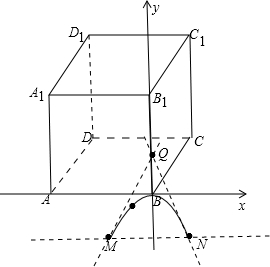：解：如图，以AB所在直线为x轴，BB₁所在直线为y轴建立平面直角坐标系，
设P（x，y），由题意可得，x²+a²=（a-y）²（y≤0），
所以P点的轨迹是双曲线的一支，
因为|B1E|=

2

|B1B|=

2

a，所以E点的纵坐标为a-

2

a，
代入双曲线方程得：M（-a，a-

2

a），N（a，a-

2

a）．
设过M点的曲线的切线的斜率为k，则：切线方程为y=a-

2

a+k(x+a)，
与双曲线方程联立得：(k2-1)x2+2k(ak-

2

a)x+a2k2-2

2

a2k+a2=0
由△=4k2(ak-

2

a)2-4(k2-1)(a2k2-2

2

a2k+a2)=8a2k2-8

2

a2k+4a2=0
得：2k2-2

2

k+1=0，所以k=

2

2

，
把k=

2

2

代入切线方程并取x=0得：y=a-

2

2

a，即Q点的纵坐标为a-

2

2

a，
所以三角形MNQ的高为

2

2

a，
所以S△MNQ=

1

2

×2a×

2

2

a=

2

2

a2．
故选D．

点评：本题考查了棱柱的结构特征，考查了数学转化思想和方程思想，考查了圆锥曲线知识，训练了学生的运算能力，正确得到点P的轨迹是该题的难点，此题有一定难度．