题目内容
已知函数![]()
(1)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求
时,求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(3)当![]() 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数![]() ,都有
,都有 ![]()
同下
解析:
(1)∵ ![]() ∴
∴ ![]() ……………1分
……………1分
∵ 函数![]() 在
在![]() 上为增函数
上为增函数
∴ ![]() 对
对![]() 恒成立, ……2分
恒成立, ……2分
∴ ![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立
恒成立
∴ ![]() ………4分
………4分
(2)当![]() 时,
时,![]() ,
,
∴ 当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增, ……6分
上单调递增, ……6分
∴ ![]() 在区间
在区间![]() 上有唯一极小值点,故
上有唯一极小值点,故![]() …7分
…7分
又 ![]()
∵ ![]() ∴
∴ ![]()
∴ ![]() 在区间
在区间![]() 上的最大值
上的最大值![]()
综上可知,函数![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是0. ………………9分
,最小值是0. ………………9分
(3)当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 在
在![]() 上为增函数。
上为增函数。
当![]() 时,令
时,令![]() ,则
,则![]() ,故
,故![]() ……………11分
……………11分
∴ 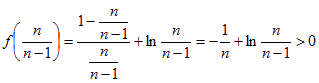 ,即
,即![]() ……12分
……12分
∴ ![]()
∴ ![]() ……………13分
……………13分
∴ ![]()
即对大于1的任意正整数![]() ,都有
,都有 ![]() ……………14分
……………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
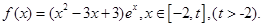
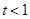 时,求函数
时,求函数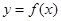 的单调区间;
的单调区间;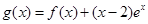 ,试问函数
,试问函数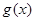 在
在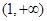 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.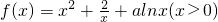 ,
,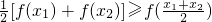 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.