题目内容
已知函数![]() 为奇函数,且
为奇函数,且![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
⑴求函数![]() 的解析式;
的解析式;
⑵记![]() ,求
,求![]() 的单调区间.
的单调区间.
解:⑴由![]() 为奇函数,∴
为奇函数,∴![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() 在
在![]() 处取得极大值
处取得极大值![]() .∴
.∴![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() .经检验符合题意,故
.经检验符合题意,故![]() …………5分
…………5分
⑵由⑴知![]() ,∴
,∴![]() .
.
易知函数![]() 的定义域为
的定义域为![]() . ………7分
. ………7分
①当![]() ,即
,即![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减;……8分
上单调递减;……8分
②当![]() ,即
,即![]() 时,∵
时,∵![]() ,∴
,∴![]() ,
,
∴函数![]() 在
在![]() 上单调递减; ………………9分
上单调递减; ………………9分
③当![]() ,即
,即![]() 时,令
时,令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
结合![]() ,得
,得![]() ;令
;令![]() ,同上得
,同上得![]() ,∴
,∴![]() ,
,
∴![]() 时, 函数
时, 函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
综上,当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,无单调递增区间;
,无单调递增区间;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() . ………13分
. ………13分

练习册系列答案
相关题目
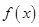 为奇函数,且当
为奇函数,且当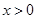 时,
时,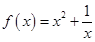 ,则
,则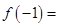 ( )
( )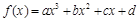 为奇函数,且在
为奇函数,且在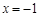 处取得极大值2.
处取得极大值2.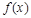 的解析式;
的解析式;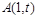 (
(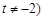 可作函数
可作函数 图像的三条切线,求实数
图像的三条切线,求实数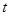 的取值范围;
的取值范围;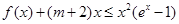 对于任意的
对于任意的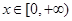 恒成立,求实数
恒成立,求实数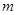 的取值范围.
的取值范围. 为奇函数,且
为奇函数,且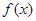 在
在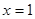 处取得极大值2.(1)求函数
处取得极大值2.(1)求函数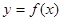 的解析式;
的解析式;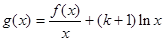 ,求函数
,求函数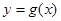 的单调区间;
的单调区间;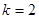 时,若函数
时,若函数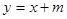 的下方,求
的下方,求 的取值范围。
的取值范围。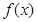 为奇函数,且
为奇函数,且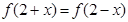 ,当
,当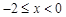 时,
时,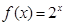 ,
,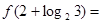 。
。 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数