题目内容
如图,已知正三棱柱ABC—A1B1C1的侧棱与底面边长皆为2,D是BC的中点,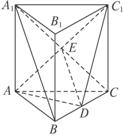
(1)求证:A1B∥平面C1AD;
(2)求直线A1B与平面C1AD间的距离;
(3)求二面角C-AC1-D的大小.
解法一:(1)证明:连结A1C交AC1于点E,连结ED.在△A1BC中,E、D分别为A1C、CB的中点,有ED∥A1B.

又ED![]() 平面C1AD,A1B
平面C1AD,A1B![]() 平面C1AD,
平面C1AD,
∴A1B∥平面C1AD.
(2)易证AD⊥平面B1BCC1.又AD![]() 平面C1AD,则平面C1AD⊥平面B1BCC1,且C1D为这两个互相垂直平面的交线.
平面C1AD,则平面C1AD⊥平面B1BCC1,且C1D为这两个互相垂直平面的交线.
由于A1B∥平面C1AD,则直线A1B与平面C1AD的距离等于点B到平面C1AD的距离,等于点B到直线C1D的距离.
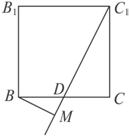
作BM⊥C1D交C1D的延长线于M,可求得BM=![]() .
.
(3)由于平面B1BCC1⊥平面C1AD,过C作CF⊥C1D于F,交C1D于F,则CF⊥平面C1AD,连结EF,则∠CEF为所求.可求得CE=![]() ,CF=
,CF=![]() ,在Rt△CEF中,sin∠CEF=
,在Rt△CEF中,sin∠CEF=![]() =
=![]() ,
,
∴二面角CAC1D的平面角为arcsin![]() . 1
. 1
解法二:如图建立空间直角坐标系,可求出如下各点的坐标:
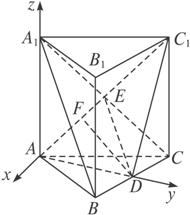
A(0,0,0),A1(0,0,2),B(1,![]() ,0),B1(1,
,0),B1(1,![]() ,2),C(-1,
,2),C(-1,![]() ,0),C1(-1,
,0),C1(-1,![]() ,2),D(0,
,2),D(0,![]() ,0).
,0).
(1)证明:连结A1C交AC1于E,连结ED.
则E(-![]() ,
,![]() ,1),
,1),![]() =(1,
=(1,![]() ,-2),
,-2),![]() =(
=(![]() ,
,![]() ,-1),有
,-1),有![]() =2
=2![]() ,则
,则![]() ∥
∥![]() .
.
又A1B与B1D不共线,则A1B∥ED.
(2)同解法一.
(3)易证![]() ⊥
⊥![]() ,
,![]() =(-
=(-![]() ,
,![]() ,-1),作DF⊥AC1于F,设F(x,y,z),
,-1),作DF⊥AC1于F,设F(x,y,z),
则![]() =(-x,
=(-x,![]() -y,-z),又
-y,-z),又![]() =(1,-
=(1,-![]() ,-2),
,-2),![]() =(-x,-y,-z),
=(-x,-y,-z),
由![]() 与
与![]() 共线,得x=-λ,y=
共线,得x=-λ,y=![]() λ,z=2λ,
λ,z=2λ,
则![]() =(λ,
=(λ, ![]() -
-![]() λ,-2λ).
λ,-2λ).
由![]() ⊥
⊥![]() ,得λ-3+3λ+4λ=0.
,得λ-3+3λ+4λ=0.
解之,得λ=![]() .∴
.∴![]() =(
=(![]() ,
,![]() ,-
,-![]() ).
).
则cos〈![]() ,
,![]() 〉=
〉=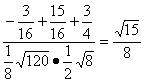 .
.
∴二面角的平面角为arccos![]() .
.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为