题目内容
已知tanα=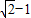 函数f(x)=
函数f(x)= 其中
其中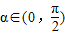
(1)求f(x)的解析式;
(2)若数列{an}满足
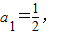 an+1=f(an)(n∈N*)求证:
an+1=f(an)(n∈N*)求证:(i)an+1>an(n∈N*);
(ii)1<
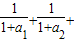 …+
…+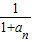 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).
【答案】分析:(1)由tan2α=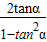 =
=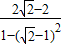 =1,将tanα=
=1,将tanα=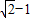 代入可求解,由α为锐角,得α,进而求得函数表达式.
代入可求解,由α为锐角,得α,进而求得函数表达式.
(2)(i)由数列{an}满足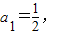 an+1=f(an)(n∈N*),知
an+1=f(an)(n∈N*),知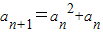 ,由此能够证明an+1>an(n∈N*).
,由此能够证明an+1>an(n∈N*).
(ii)由数列{an}满足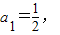 ,
,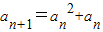 =an(an+1),能够导出
=an(an+1),能够导出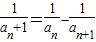 ,利用裂项求和法得到
,利用裂项求和法得到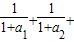 …+
…+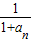 =2-
=2-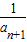 ,由此能够证明1<
,由此能够证明1<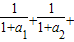 …+
…+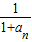 <2(n≥2,n∈N*)
<2(n≥2,n∈N*)
解答:解:(1)解:∵tan2α=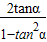 =
=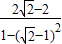 =1
=1
又∵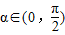 ,
,
∴α=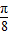 ,∴sin(2α+
,∴sin(2α+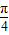 )=1,
)=1,
∴f(x)=x2+x.
(2)(i)∵数列{an}满足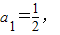 an+1=f(an)(n∈N*),
an+1=f(an)(n∈N*),
∴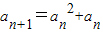 ,
,
∴an+1-an=an2>0,
∴an+1>an(n∈N*).
(ii)∵数列{an}满足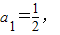 ,
,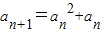 =an(an+1),
=an(an+1),
∴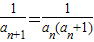 =
=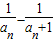 ,
,
∴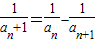 ,
,
∴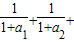 …+
…+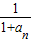 =(
=(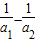 )+(
)+(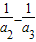 )+…+(
)+…+(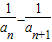 )
)
=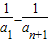
=2-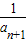 ,
,
∴1<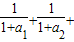 …+
…+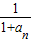 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).
点评:本题考查函数解析式的求法和不等式的证明,具体涉及到正切函数的倍角公式、数列与函数、数列与不等式的综合,解题时要认真审题,仔细解答,注意裂项求和法的合理运用.
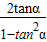 =
=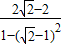 =1,将tanα=
=1,将tanα=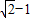 代入可求解,由α为锐角,得α,进而求得函数表达式.
代入可求解,由α为锐角,得α,进而求得函数表达式.(2)(i)由数列{an}满足
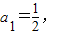 an+1=f(an)(n∈N*),知
an+1=f(an)(n∈N*),知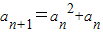 ,由此能够证明an+1>an(n∈N*).
,由此能够证明an+1>an(n∈N*).(ii)由数列{an}满足
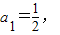 ,
,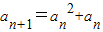 =an(an+1),能够导出
=an(an+1),能够导出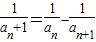 ,利用裂项求和法得到
,利用裂项求和法得到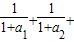 …+
…+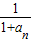 =2-
=2-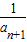 ,由此能够证明1<
,由此能够证明1<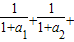 …+
…+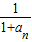 <2(n≥2,n∈N*)
<2(n≥2,n∈N*)解答:解:(1)解:∵tan2α=
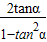 =
=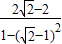 =1
=1又∵
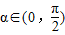 ,
,∴α=
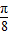 ,∴sin(2α+
,∴sin(2α+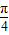 )=1,
)=1,∴f(x)=x2+x.
(2)(i)∵数列{an}满足
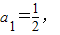 an+1=f(an)(n∈N*),
an+1=f(an)(n∈N*),∴
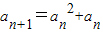 ,
,∴an+1-an=an2>0,
∴an+1>an(n∈N*).
(ii)∵数列{an}满足
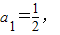 ,
,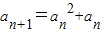 =an(an+1),
=an(an+1),∴
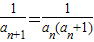 =
=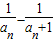 ,
,∴
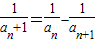 ,
,∴
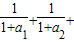 …+
…+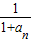 =(
=(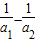 )+(
)+(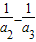 )+…+(
)+…+(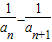 )
)=
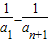
=2-
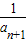 ,
,∴1<
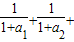 …+
…+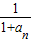 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).点评:本题考查函数解析式的求法和不等式的证明,具体涉及到正切函数的倍角公式、数列与函数、数列与不等式的综合,解题时要认真审题,仔细解答,注意裂项求和法的合理运用.

练习册系列答案
相关题目
 .
.