题目内容
已知函数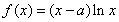 ,
,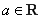 .
.
(Ⅰ)当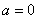 时,求函数
时,求函数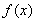 的极小值;
的极小值;
(Ⅱ)若函数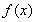 在
在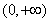 上为增函数,求
上为增函数,求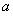 的取值范围.
的取值范围.
【答案】
(Ⅰ)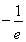 ;(Ⅱ)
;(Ⅱ)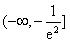
【解析】
试题分析:(Ⅰ)先求导数,及其零点,判断导数符号变化,即可得原函数增减变化,可得其极值。(Ⅱ)函数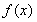 在
在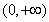 是增函数,转化为
是增函数,转化为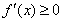 ,对
,对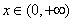 恒成立问题。即
恒成立问题。即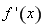 的最小值大于等于0.将问题最终转化为求
的最小值大于等于0.将问题最终转化为求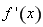 的最小值问题。仍用导数求单调性,用单调性求最值的方法求
的最小值问题。仍用导数求单调性,用单调性求最值的方法求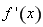 的最小值。所以需设函数
的最小值。所以需设函数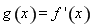 ,对函数
,对函数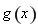 重新求导,求极值。判断导数符号变化,得
重新求导,求极值。判断导数符号变化,得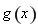 的增减区间,的最小值。
的增减区间,的最小值。
试题解析:解:(Ⅰ)定义域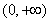 .
.
当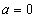 时,
时,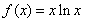 ,
,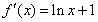 .
.
令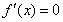 ,得
,得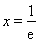 .
.
当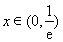 时,
时,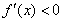 ,
,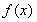 为减函数;
为减函数;
当 时,
时,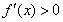 ,
,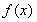 为增函数.
为增函数.
所以函数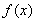 的极小值是
的极小值是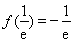 . 5分
. 5分
(Ⅱ)由已知得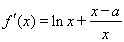 .
.
因为函数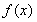 在
在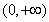 是增函数,所以
是增函数,所以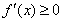 ,对
,对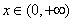 恒成立.
恒成立.
由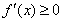 得
得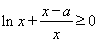 ,即
,即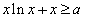 对
对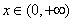 恒成立.
恒成立.
设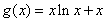 ,要使“
,要使“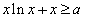 对
对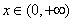 恒成立”,只要
恒成立”,只要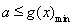 .
.
因为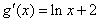 ,令
,令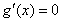 得
得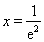 .
.
当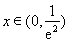 时,
时,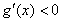 ,
,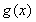 为减函数;
为减函数;
当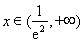 时,
时,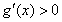 ,
,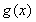 为增函数.
为增函数.
所以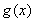 在
在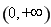 上的最小值是
上的最小值是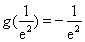 .
.
故函数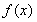 在
在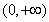 是增函数时,实数
是增函数时,实数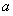 的取值范围是
的取值范围是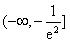 13分
13分
考点:1函数的概念和性质;2导数和利用导数研究函数性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目