题目内容
已知函数 ,(
,( 为常数,
为常数, 为自然对数的底).
为自然对数的底).
(Ⅰ)当 时,求
时,求 ;
;
(Ⅱ)若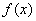 在
在 时取得极小值,试确定
时取得极小值,试确定 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设由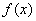 的极大值构成的函数为
的极大值构成的函数为 ,将
,将 换元为
换元为 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
(  为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由.
解:(Ⅰ)当 时,
时, .
. .
.
所以 .
.
(Ⅱ)
 .
.
令 ,得
,得 或
或 .
.
当 ,即
,即 时,
时,
 恒成立,
恒成立,
此时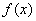 在区间
在区间 上单调递减,没有极小值;
上单调递减,没有极小值;
当 ,即
,即 时,
时,
若 ,则
,则 .若
.若 ,则
,则 .
.
所以 是函数
是函数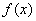 的极小值点.
的极小值点.
当 ,即
,即 时,
时,
若 ,则
,则 .若
.若 ,则
,则 .
.
此时 是函数
是函数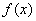 的极大值点.
的极大值点.
综上所述,使函数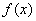 在
在 时取得极小值的
时取得极小值的 的取值范围是
的取值范围是 .
.
(Ⅲ)由(Ⅱ)知当 ,且
,且 时,
时, ,
,
因此 是
是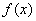 的极大值点,极大值为
的极大值点,极大值为 .
.
所以 .
.  .
.
令 .
.
则 恒成立,即
恒成立,即 在区间
在区间 上是增函数.
上是增函数.
所以当 时,
时, ,即恒有
,即恒有 .
.
又直线 的斜率为
的斜率为 ,
,
所以曲线 不能与直线
不能与直线 相切.
相切.

练习册系列答案
相关题目
观察两个变量x,y,得到的数据如下表:
| x | 2 | 4 | 6 | 8 | 10 |
| y | 64 | 138 | 205 | 285 | 360 |
(1)对变量y与x进行相关性检验;
(2)如果y与x之间具有线性相关关系,求回归直线方程.
【解】 (1)r=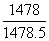 ≈0.999 7,r0.05=0.878.r>r0.05,故y与x之间显著线性相关
≈0.999 7,r0.05=0.878.r>r0.05,故y与x之间显著线性相关
(2) 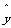 =36.95x-11.3.
=36.95x-11.3.
11.高二(3)班学生每周用于数学学习的时间x(单位:小时)与数学成绩Y(单位:分)之间有如下数据:
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| Y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
若某同学每周用于数学学习的时间为18小时,试预测该同学数学成绩.
 =x
=x +y
+y ,则x=________,y=________.
,则x=________,y=________.
 ,若
,若 对应的点在直线
对应的点在直线 上,则
上,则 的值是 .
的值是 . 及曲线
及曲线 所围成的封闭的图形的面积为
所围成的封闭的图形的面积为 B.
B. C.
C. D.
D.
 满足
满足 (
( 为虚数单位),复数
为虚数单位),复数 的虚部为
的虚部为 ,
,
 是实数,求
是实数,求 与直线y – x – 2 = 0围成图形的面积是( ) .
与直线y – x – 2 = 0围成图形的面积是( ) . B、
B、 C、
C、 D、
D、
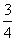 ,则P(η≥1)=________.
,则P(η≥1)=________.