题目内容
过双曲线 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于
的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于 ,则双曲线的离心率e=________.
,则双曲线的离心率e=________.
2
分析:先根据三角形面积公式求得a,b和c的关系式,进而根据a= 求得a和c的关系式,进而求得e.
求得a和c的关系式,进而求得e.
解答:∵S△ABF= ×
× ×|FB|=
×|FB|= b•|AF|,
b•|AF|,
∴
 =(c-a)b
=(c-a)b
∴b2+c2=7(c-a)2,
整理得5e2-14e+8=0,解得e=2
故答案为:2
点评:本题主要考查了双曲线的简单性质.解题的关键是找到a和c的关系,进而求得双曲线的离心率.
分析:先根据三角形面积公式求得a,b和c的关系式,进而根据a=
 求得a和c的关系式,进而求得e.
求得a和c的关系式,进而求得e.解答:∵S△ABF=
 ×
× ×|FB|=
×|FB|= b•|AF|,
b•|AF|,∴

 =(c-a)b
=(c-a)b∴b2+c2=7(c-a)2,
整理得5e2-14e+8=0,解得e=2
故答案为:2
点评:本题主要考查了双曲线的简单性质.解题的关键是找到a和c的关系,进而求得双曲线的离心率.

练习册系列答案
相关题目
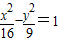 与椭圆
与椭圆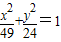 有相同的焦点;
有相同的焦点;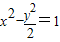 的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.
的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条. 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于
的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于 ,则双曲线的离心率e= .
,则双曲线的离心率e= . 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于
的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于 ,则双曲线的离心率e= .
,则双曲线的离心率e= . 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于
的右焦点F和虚轴端点B作一条直线,若右顶点A到直线FB的距离等于 ,则双曲线的离心率e= .
,则双曲线的离心率e= .