题目内容
已知a、b是两个非零向量,同时满足|a|=|b|=|a-b|,求a与a+b的夹角.
思路分析:根据向量夹角公式得:cosθ=![]() ,须根据已知条件找到a·b与a的关系.|a+b|与|a|的关系即可解决.
,须根据已知条件找到a·b与a的关系.|a+b|与|a|的关系即可解决.
解法1:
根据|a|=|b|,有|a|2=|b|2.
又由|b|=|a-b|,得|b|2=|a|2-2a·b+|b|2,
∴a·b=![]() |a|2.
|a|2.
而|a+b|2=|a|2+2a·b+|b|2=3|a|2,
∴|a+b|=![]() |a|.
|a|.
设a与a+b的夹角为θ,则
cosθ=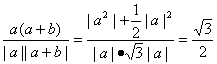 .
.
∴θ=30°
解法2:
设向量a=(x1,y1),b=(x2,y2).
∵|a|=|b|,∴x12+y12=x22+y22.
由|b|=|a-b|,得x1x2+y1y2=![]() (x12+y12).
(x12+y12).
即a·b=![]() (x12+y12).
(x12+y12).
由|a+b|2=2(x12+y12)+2×![]() (x12+y12)=3(x12+y12),得|a+b|=
(x12+y12)=3(x12+y12),得|a+b|=![]() .
.
设a与a+b的夹角为θ,则cosθ=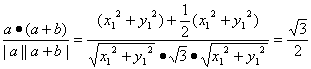 .
.
∴θ=30°.
解法3:根据向量加法的几何意义,作图如下图
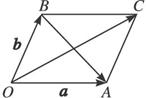
在平面内任取一点O,作![]() =a,
=a,![]() =b,以
=b,以![]() 、
、![]() 为邻边作平行四边形OACB.
为邻边作平行四边形OACB.
∵|a|=|b|,即|![]() |=|
|=|![]() |,
|,
∴平行四边形OACB为菱形,OC平分∠AOB.
这时![]() =a+b,
=a+b,![]() =a-b.
=a-b.
而|a|=|b|=|a-b|,
即|![]() |=|
|=|![]() |=|
|=|![]() |.
|.
∴△AOB为正三角形,则∠AOB=60°.
于是∠AOC=30°,即a与a+b的夹角为30°.
温馨提示
基于平面向量的表示上的差异,也就是表示方法的不同,才产生了以上三种不同解法.对于本题的三种解法都要认真理解.

练习册系列答案
相关题目
已知
,
是两个非零向量,给定命题p:|
+
|=|
|+|
|;命题q:?t∈R,使得
=t
;则p是q的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知
、
是两个非零向量,且|
|=|
|=|
-
|,则
与
+
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、30° | B、60° |
| C、90° | D、150° |