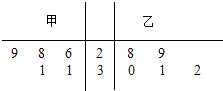题目内容
【题目】若[x]表示不超过x的最大整数，则[lg2]+[lg3]+…+lg[2017]+[lg 
]+[lg 
]+…+[lg 
]= ．
【答案】-2013
【解析】解：当2≤n≤9时，[lgn]=0，
当10≤n≤99时，[lgn]=1，
当100≤n≤999时，[lgn]=2，
当1000≤n≤9999时，[lgn]=3，
故[lg2]+[lg3]+…+[lg2016]+[2017]
=0×8+1×90+2×900+3×1018
=90+1800+3054
=4944；
当 
≤ 
≤ 
，[lg ]=﹣1；
当 
≤ ≤ 
时，[lg ]=﹣2；
当 
≤ ≤ 
时，[lg ]=﹣3；
当 
≤ ≤ 
时，[lg ]=﹣4．
则[lg ]+[lg 
]+…+[lg 
]
=（﹣1）×9+（﹣2）×90+（﹣3）×900+（﹣4）×1017
=﹣6957，
故原式=4944﹣6957=﹣2013．
所以答案是：﹣2013．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系
)．
练习册系列答案
相关题目
