题目内容
已知抛物线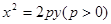 的焦点为
的焦点为 ,点
,点 为抛物线上的一点,其纵坐标为
为抛物线上的一点,其纵坐标为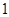 ,
,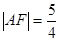 .
.
(1)求抛物线的方程;
(2)设 为抛物线上不同于
为抛物线上不同于 的两点,且
的两点,且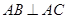 ,过
,过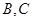 两点分别作抛物线的切线,记两切线的交点为
两点分别作抛物线的切线,记两切线的交点为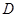 ,求
,求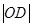 的最小值.
的最小值.
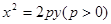 的焦点为
的焦点为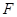 ,点
,点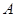 为抛物线上的一点,其纵坐标为
为抛物线上的一点,其纵坐标为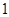 ,
,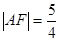 .
.(1)求抛物线的方程;
(2)设
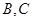 为抛物线上不同于
为抛物线上不同于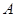 的两点,且
的两点,且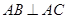 ,过
,过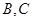 两点分别作抛物线的切线,记两切线的交点为
两点分别作抛物线的切线,记两切线的交点为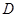 ,求
,求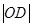 的最小值.
的最小值.(1)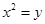 ;(2)
;(2)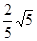 .
.
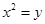 ;(2)
;(2)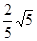 .
.试题分析:(1)对于开口向上的抛物线来说,
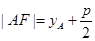 ,代入坐标,解出
,代入坐标,解出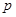 ;
;(2)设
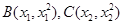 ,利用导数的几何意义,利用点斜式方程,分别设出过
,利用导数的几何意义,利用点斜式方程,分别设出过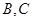 两点的切线方程,然后求出交点
两点的切线方程,然后求出交点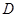 的坐标,结合
的坐标,结合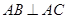 ,所得到的关系式
,所得到的关系式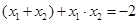 ,设
,设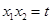 ,以及
,以及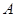 的坐标,将点
的坐标,将点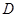 的坐标转化为一个未知量
的坐标转化为一个未知量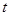 表示的函数,,用未知量表示
表示的函数,,用未知量表示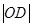 ,转化为函数的最值问题,利用二次函数求最值的方法求出.中档偏难题型.
,转化为函数的最值问题,利用二次函数求最值的方法求出.中档偏难题型.试题解析:(1)由抛物线定义得:
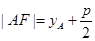
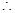
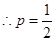 2分
2分 抛物线方程为
抛物线方程为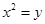 4分
4分(2)设
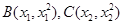
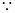
 且
且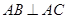
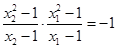 即
即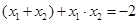 6分
6分又
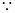
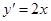
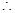
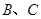 处的切线的斜率为
处的切线的斜率为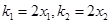
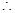
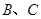 处的切线方程为
处的切线方程为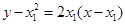 和
和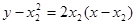
由
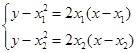 得
得 8分
8分设
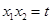 ,由
,由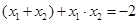 得
得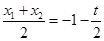
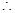
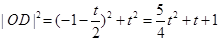 10分
10分当
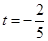 时,
时,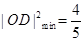
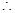
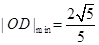 12分
12分
练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,
, 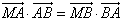 ,M点的轨迹为曲线C。
,M点的轨迹为曲线C。 ,4),则|PA|+|PM|的最小值是
,4),则|PA|+|PM|的最小值是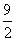
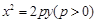 ,过点
,过点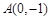 作直线
作直线 与抛物线相交于
与抛物线相交于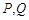 两点,点
两点,点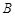 的坐标为
的坐标为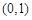 ,连接
,连接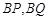 ,设
,设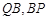 与
与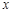 轴分别相交于
轴分别相交于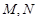 两点.如果
两点.如果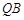 的斜率与
的斜率与 的斜率的乘积为
的斜率的乘积为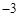 ,则
,则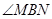 的大小等于.
的大小等于.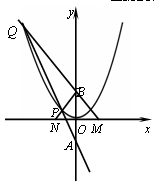
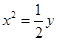 的焦点到准线的距离是( )
的焦点到准线的距离是( )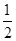
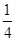
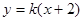 (k>0)与抛物线
(k>0)与抛物线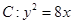 相交于
相交于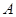 、
、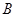 两点,
两点,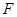 为
为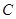 的焦点,若
的焦点,若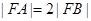 ,则k的值为
,则k的值为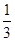
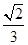
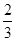
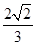
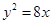 的准线方程是 .
的准线方程是 .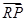 ·
·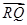 的最小值.
的最小值.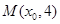 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点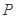 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点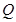 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线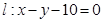 上的点
上的点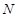 ,经直线反射后又回到点
,经直线反射后又回到点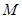 ,则
,则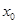 等于( )
等于( )