题目内容

如图，F1、F2分别是双曲线x2-y2=1的左、右焦点，点A的坐标是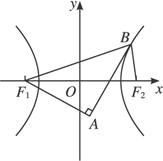（,-）,点B在双曲线上，且·=0.

（1）求点B的坐标；

（2）求证：∠F1BA=∠F2BA.

（1）解析：依题意知F1（-2,0）,F2(2,0),?A(,-).

设B（x0,y0）,则=(,-),?=(x0-,y0+),

∵·=0，

∴(x0-)-(y0+)=0,

即3x0-y0=2.

又∵x02-y02=1,

∴x02-(3x0-2)2=1,

(2x0-3)2=0.

∴x0=,代入3x0-y0=2,得y0=.

∴点B的坐标为（,）.

（2）证明：=(-,-),?BF2=(,-),=(-,-),

cosF1BA=,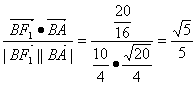

cosF2BA=,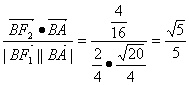

∴∠F1BA=∠F2BA.

练习册系列答案
相关题目
精英家教网如图，F1，F2分别为椭圆
x2
a2
+
y2
b2
=1的左、右焦点，点P在椭圆上，△POF2是面积为
3
的正三角形，则b2的值是
 
．
如图，F1、F2分别为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点，椭圆的右准线l与x轴交于A点，若F1（-1，0），且
AF1
=2
AF2
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过F1、F2作互相垂直的两直线分别与椭圆交于P、Q、M、N四点，求四边形PMQN面积的取值范围．
如图，F1，F2分别为双曲线
x2
a2
-
y2
b2
=1的左右焦点，点P在双曲线上，若△POF2是面积为1的正三角形，则b2的值为（　　）
如图，F1、F2分别为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点，椭圆的右准线l与x轴交于A点，若F1（-1，0），且
AF1
=2
AF2
．
（I）求椭圆的方程；
（II）过F1、F2作互相垂直的两直线分别与椭圆交于P、Q、M、N四点，若直线MN的倾斜角为
π
4
，求四边形PMQN的面积．

如图，F1，F2分别为椭圆的左、右焦点，点P在椭圆上，△POF2是面积

为的正三角形，则的值是     

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网