题目内容
选修4-5:不等式选讲
证明: +
+ +
+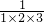 +…+
+…+ <2(n>2,n∈N*).
<2(n>2,n∈N*).
证明: +
+ +
+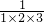 +…+
+…+ <1+
<1+ +
+ +…+
+…+
=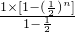 =2×[1-
=2×[1- ]=2-
]=2- <2.
<2.
故要证的不等式成立.
分析:利用 n>2,n∈N*时, <
< ,把不等式的左边从第三项开始,每项都放大为
,把不等式的左边从第三项开始,每项都放大为 ,
,
再利用等比数列的求和公式运算,结果为2- ,显然小于2成立.
,显然小于2成立.
点评:本题考查不等式的放缩,等比数列的求和公式,不等式的放缩是解题的难点.
 +
+ +
+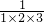 +…+
+…+ <1+
<1+ +
+ +…+
+…+
=
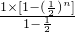 =2×[1-
=2×[1- ]=2-
]=2- <2.
<2.故要证的不等式成立.
分析:利用 n>2,n∈N*时,
 <
< ,把不等式的左边从第三项开始,每项都放大为
,把不等式的左边从第三项开始,每项都放大为 ,
,再利用等比数列的求和公式运算,结果为2-
 ,显然小于2成立.
,显然小于2成立.点评:本题考查不等式的放缩,等比数列的求和公式,不等式的放缩是解题的难点.

练习册系列答案
相关题目