题目内容
设圆C的圆心在双曲线| x2 |
| a2 |
| y2 |
| 2 |
| 3 |
分析:先利用圆与双曲线的渐近线相切得圆的半径,再利用圆C被直线l:x-
y=0截得的弦长等于2,求出a与圆心到直线l:x-
y=0的距离d之间的等量关系即可求出a.
| 3 |
| 3 |
解答:解:设圆心坐标为(
,0),因为双曲线的渐近线y=
x?
x-ay=0.
由圆与双曲线的渐近线相切得圆心到直线的距离等于半径,即得r=
=
,
又因为圆C被直线l:x-
y=0截得的弦长等于2,
故圆心到直线l:x-
y=0的距离d=1=
?a2=2又a>0,故a=
.
故答案为
.
| a2+2 |
| ||
| a |
| 2 |
由圆与双曲线的渐近线相切得圆心到直线的距离等于半径,即得r=
| ||||
|
| 2 |
又因为圆C被直线l:x-
| 3 |
故圆心到直线l:x-
| 3 |
| ||||
|
| 2 |
故答案为
| 2 |
点评:本题主要考查椭圆与双曲线的几何性质,直线的方程,直线与圆的位置关系以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线 截得的弦长等于2,则
截得的弦长等于2,则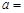 ( )
( )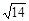 (B)
(B) (C)
(C) (D)2
(D)2 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线 截得的弦长等于2,则a的值为 ( )
截得的弦长等于2,则a的值为 ( ) B.
B. C.2 D.3
C.2 D.3 (a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l:
(a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l: 截得的弦长等于2,则a= .
截得的弦长等于2,则a= .