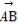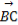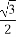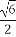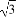Question

设函数y=sin(ωx+φ)(ω>0,φ∈(-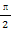,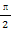))的最小正周期为π,且其图象关于直线x=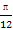对称,则在下面四个结论中:

①图象关于点(,0)对称;

②图象关于点(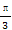,0)对称;

③在[0,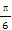]上是增函数;

④在[-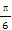,0]上是增函数.

正确结论的编号为　　　　.

 

Answer 1

②④

【解析】∵y=sin(ωx+φ)最小正周期为π,

∴ω==2.又其图象关于直线x=对称,

∴2×+φ=kπ+(k∈Z).

∴φ=kπ+,k∈Z.

由φ∈(-,),得φ=,

∴y=sin(2x+).令2x+=kπ(k∈Z),

得x=-(k∈Z).

∴y=sin(2x+)关于点(,0)对称,故②正确.

令2kπ-≤2x+≤2kπ+(k∈Z),得

kπ-≤x≤kπ+(k∈Z),

∴函数y=sin(2x+)的单调递增区间为[kπ-,kπ+](k∈Z).

∵[-,0][kπ-,kπ+](k∈Z),

∴④正确.