题目内容
已知等差数列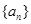 的公差
的公差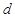 大于0,且
大于0,且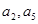 是方程
是方程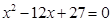 的两根,数列
的两根,数列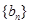 的前
的前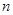 项和为
项和为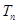 ,且
,且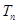
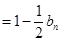
(1)求数列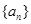 、
、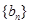 的通项公式;
的通项公式;
(2)设数列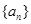 的前
的前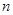 项和为
项和为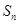 ,试比较
,试比较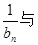
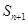 的大小,并说明理由.
的大小,并说明理由.
【答案】
解:(1)
 当
当  ,
,


即
(2)




猜想:
下面用数学归纳法证明:
(Ⅰ)当 时,已知结论成立;
时,已知结论成立;
(Ⅱ)假设
 时,
时, ,即
,即
那么,当 时,
时,


故 时,
时, 也成立.
也成立.
综上,由(Ⅰ)(Ⅱ)可知 时,
时, 也成立.
也成立.
综上所述,当
 ,
, 时,
时, .
.
【解析】略

练习册系列答案
相关题目
 的公差为
的公差为 ,前
,前 项和为
项和为 ,且满足
,且满足 ,
, 表示不等式组
表示不等式组 ,并在给定的坐标系中画出不等式组表示的平面区域;
,并在给定的坐标系中画出不等式组表示的平面区域; 的最大值,并指出此时数列
的最大值,并指出此时数列 [
[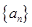 的公差
的公差 ,若
,若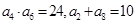 ,则该数列的前
,则该数列的前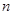 项和
项和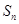 的最大值是( )
的最大值是( )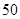 B.
B.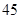 C.
C.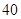 D.
D.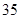
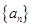 的公差
的公差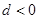 ,前
,前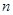 项和
项和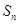 满足:
满足: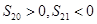 ,那么数列
,那么数列 中最大的值是(
)
中最大的值是(
)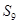 B.
B.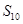 C.
C.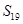 D.
D.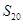
 的公差
的公差 ,若
,若 ,则该数列的前
,则该数列的前 项和
项和 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 的公差为负数,且
的公差为负数,且 ,若
,若 经重新排列后依次可成等比数列,求⑴数列
经重新排列后依次可成等比数列,求⑴数列 ;⑵数列
;⑵数列 项和
项和 的最大值。
的最大值。