题目内容
(本题满分14分)数列![]() 满足
满足![]()
![]() .
.
(1)求数列{![]() }的通项公式;(2)设数列{
}的通项公式;(2)设数列{![]() }的前
}的前![]() 项和为
项和为![]() ,证明
,证明![]() .
.
(1)![]()
解析:
(1)方法一:∵![]() ,∴
,∴![]() . --3分
. --3分
∴![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.-4分∴
的等差数列.-4分∴![]() ,所以
,所以![]() .6分
.6分
方法二:![]() ,
,![]() ,
,![]() ,猜测
,猜测![]() . -----2分
. -----2分
下用数学归纳法进行证明.
①当![]() 时,由题目已知可知
时,由题目已知可知![]() ,命题成立; --------------3分
,命题成立; --------------3分
②假设当![]() (
(![]() )时成立,即
)时成立,即![]() ,那么
,那么
当![]() ,
,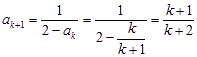 ,也就是说,当
,也就是说,当![]() 时命题也成立. ----5分
时命题也成立. ----5分
综上所述,数列![]() 的通项公式为
的通项公式为![]() . ---6分
. ---6分
(2) 设![]() 则
则![]() --------8分
--------8分
∴函数![]() 为
为![]() 上的减函数,∴
上的减函数,∴![]() ,即
,即![]()
从而 ![]() -----10分
-----10分
![]() ----------11分
----------11分
![]() ---13分
---13分
∴![]() ----------14分
----------14分

(本题满分14分) 某中学为了解学生的睡眠情况与学习效率的关系,从中抽取20名学生作为样本进行调查.调查的数据整理分组如下表示:
|
睡眠时间(单位:小时) |
|
|
|
|
|
|
|
频 数 |
1 |
3 |
|
6 |
4 |
|
|
频 率 |
|
|
0.20 |
|
|
|
(1)将以上表格补充完整,

(2)在给定的坐标系内画出样本的频率分布直方图;
(3)为了比较睡眠情况与学习效率的关系,现从睡眠时间在 与
与 个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?

 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数. ,求
,求 的值;
的值;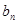 ,求证
,求证 .(本题满分14分)
.(本题满分14分) 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数








