题目内容
已知p:∀x∈R,2x>m(x2+1),q:∃x0∈R,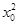 +2x0-m-1=0,且p∧q为真,求实数m的取值范围.
+2x0-m-1=0,且p∧q为真,求实数m的取值范围.
【答案】
-2≤m<-1.
【解析】
试题分析:2x>m(x2+1) 可化为mx2-2x+m<0.
所以若p:∀x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
由此可得m的取值范围.
若q:∃x0∈R,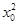 +2x0-m-1=0为真,
+2x0-m-1=0为真,
则方程x2+2x-m-1=0有实根,由此可得m的取值范围.
p∧q为真,则p、q 均为真命题,取m的公共部分便得m的取值范围.
试题解析:2x>m(x2+1) 可化为mx2-2x+m<0.
若p:∀x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
当m=0时,不等式可化为-2x<0,显然不恒成立;
当m≠0时,有m<0,Δ= 4-4m2<0,∴m<-1.
若q:∃x0∈R,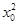 +2x0-m-1=0为真,
+2x0-m-1=0为真,
则方程x2+2x-m-1=0有实根,
∴Δ=4+4(m+1)≥0,∴m≥-2.
又p∧q为真,故p、q 均为真命题.
∴m<-1且m≥-2,∴-2≤m<-1.
考点:1、全称命题与特称命题;2、逻辑连结词.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ),3x>2x,命题q:∃x∈(
),3x>2x,命题q:∃x∈( ,0),
,0), ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )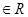 ,
,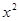 >0,则(
)
>0,则(
)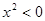 B.非p:∀x
B.非p:∀x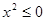
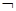 p:∃x0∈R,sin
x0≥1
p:∃x0∈R,sin
x0≥1