Question

证明三角形的三条高线交于一点.

Answer 1

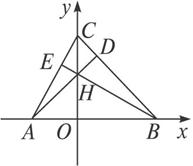
证明:如图,△ABC,则AD,BE,CO分别是△ABC的三条高,取边AB所在的直线为x轴,CO所在的直线为y轴,建立坐标系.

    设BE交AD于点H(x,y),A(-a,0,),B(b,0),C(0,c),则=(x-b,y),=(x+a,y),=(-b,c), =(a,c).

∵⊥·=0,

即a(x-b)+cy=0,①

∵⊥·=0,

故(-b)(x+a)+cy=0,②

①-②得(a+b)x=0.

∵a+b≠0,∴x=0.

∴H在AB的高线上,即△ABC三条高线交于一点.