题目内容
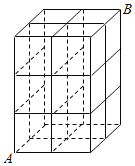
【题目】如图,在三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面,![]() ,
, ![]() 为
为![]() 的中点,过
的中点,过![]() 的平面与
的平面与![]() 交于点
交于点![]() .
.

(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)四边形![]() 是什么平面图形?说明理由,并求其面积.
是什么平面图形?说明理由,并求其面积.
【答案】(1)见解析;(2)直角梯形,![]()
【解析】
(1)利用线面平行的判定定理和性质定理,证明A1B1∥平面ABFE,A1B1∥EF,可得点F为B1C1的中点;
(2)四边形ABFE是直角梯形,先判断四边形ABFE是梯形;再判断梯形ABFE是直角梯形,从而计算直角梯形ABFE的面积.
(1)证明:三棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() ,
,
又![]() 为
为![]() 的中点,∴点
的中点,∴点![]() 为
为![]() 的中点;
的中点;
(2)四边形![]() 是直角梯形,理由为:
是直角梯形,理由为:
由(1)知,![]() ,且
,且![]() ,∴四边形
,∴四边形![]() 是梯形;
是梯形;
又侧棱B1B⊥底面ABC,∴B1B⊥AB;又AB=6,BC=8,AC=10,
∴AB2+BC2=AC2,∴AB⊥BC,又B1B∩BC=B,∴AB⊥平面B1BCC1;
又BF平面B1BCC1,∴AB⊥BF;∴梯形ABFE是直角梯形;
由BB1=3,B1F=4,∴BF=5;又EF=3,AB=6,
∴直角梯形ABFE的面积为S=![]() ×(3+6)×5=
×(3+6)×5=![]() .
.

练习册系列答案
相关题目