题目内容
| ∫ | 3 1 |
| 4-(x-2)2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
分析:由于
(
+3)dx=
dx+
3dx.前半部分由积分的几何意义求解较好,其几何意义是以(2,0)为圆心,以2为半径的圆在x从1到3部分与x轴所围成的图形的面积.
| ∫ | 3 1 |
| 4-(x-2)2 |
| ∫ | 3 1 |
| 4-(x-2)2 |
| ∫ | 3 1 |
解答: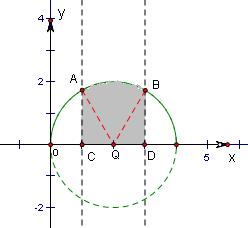 解:由于
解:由于
(
+3)dx=
dx+
3dx.
其中
dx值相当于(2,0)为圆心,以2为半径的圆在x从1到3部分与x轴所围成的图形的面积的大小,即图中阴影部分的面积.
故其值是S△ACQ+S扇形ABQ+S△BDQ=
×1×
+
×22×π+
×1×
=
+
,
又
3dx=6,
∴
(
+3)dx=
π+
+6.
故答案为:
π+
+6.
 解:由于
解:由于| ∫ | 3 1 |
| 4-(x-2)2 |
| ∫ | 3 1 |
| 4-(x-2)2 |
| ∫ | 3 1 |
其中
| ∫ | 3 1 |
| 4-(x-2)2 |
故其值是S△ACQ+S扇形ABQ+S△BDQ=
| 1 |
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 3π |
| 3 |
| 3 |
又
| ∫ | 3 1 |
∴
| ∫ | 3 1 |
| 4-(x-2)2 |
| 2 |
| 3 |
| 3 |
故答案为:
| 2 |
| 3 |
| 3 |
点评:本题考查求定积分,解题的关键是掌握住求定积分的公式以及定积分的几何意义,对于有些原函数不易求出的积分的求解,用其几何意义比较方便.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目