题目内容
若A为不等式组
表示的平面区域,当a从-1连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为( )
|
分析:先由不等式组画出其表示的平面区域,再确定动直线x+y=a的变化范围,最后由三角形面积公式解之即可.
解答: 解:如图,不等式组
解:如图,不等式组
表示的平面区域是△AOB,
动直线x+y=a(即y=-x+a)在y轴上的截距从-1变化到1,动直线x+y=a扫过A中的那部分区域是阴影部分.
又知△AOB是直角边为2的等腰直角三角形,△BDE,△AGF是斜边为1等腰直角三角形,
所以区域的面积S阴影=S△AOB-2S△BDE=
×2×2-2×
×
×
=
.
故选A.
 解:如图,不等式组
解:如图,不等式组
|
动直线x+y=a(即y=-x+a)在y轴上的截距从-1变化到1,动直线x+y=a扫过A中的那部分区域是阴影部分.
又知△AOB是直角边为2的等腰直角三角形,△BDE,△AGF是斜边为1等腰直角三角形,
所以区域的面积S阴影=S△AOB-2S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
故选A.
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若实数x,y满足不等式组
,则x-y的最小值为( )
|
| A、-2 | B、-1 | C、1 | D、2 |
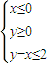 表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域面积为( )
表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域面积为( )
