题目内容
15.若数列{an}满足$\frac{1}{{{a_{n+1}}}}-\frac{2}{a_n}=0$,则称{an}为“梦想数列”,已知正项数列$\{\frac{1}{b_n}\}$为“梦想数列”,且b1+b2+b3=2,则b6+b7+b8=( )| A. | 4 | B. | 16 | C. | 32 | D. | 64 |
分析 由新定义得到数列{bn}为等比数列,由已知b1+b2+b3结合等比数列的性质得到b6+b7+b8 .
解答 解:依题意可得bn+1=2bn,则数列{bn}为等比数列,且公比为2.
∵b1+b2+b3=2,
∴b6+b7+b8=25•(b1+b2+b3)=26=64.
故选:D.
点评 本题是新定义题,考查了等比数列的性质,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知 x,y 满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤m\\ y+2x≤4\end{array}\right.$,当 3≤m≤5 时,目标函数 z=3x+2y的最大值的变化范围是( )
| A. | [7,8] | B. | [7,15] | C. | [6,8] | D. | [6,15] |
7.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
4.二次函数y=-x2-4x(x>-2)与指数函数$y={(\frac{1}{2})^x}$的交点个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
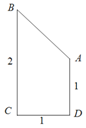 如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$.
如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$. ,若其定义域内不存在实数
,若其定义域内不存在实数 ,使得
,使得 ,则
,则 的取值范围是_____.
的取值范围是_____.