题目内容
下列函数中,值域为[0,+∞)的是
- A.

- B.y=x2+x+1
- C.

- D.
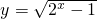
D
分析:求出各个选项中的函数的值域,与题中的条件作对比,即可得到结论.
解答:由于 ≠0,∴
≠0,∴ 的值域为{y|y>0,且y≠1},故不满足条件.
的值域为{y|y>0,且y≠1},故不满足条件.
由于y=x2+x+1= +
+ ≥
≥ ,故值域为[
,故值域为[ ,+∞),故不满足条件.
,+∞),故不满足条件.
由于 2x>0,∴ ≤1,且
≤1,且  ≥0,故函数的值域为[0,1],故不满足条件.
≥0,故函数的值域为[0,1],故不满足条件.
由于 2x>0,∴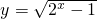 ≥0,故此函数的值域为[0,+∞),故满足条件,
≥0,故此函数的值域为[0,+∞),故满足条件,
故选D.
点评:本题主要考查二次函数、指数函数的定义域和值域,属于基础题.
分析:求出各个选项中的函数的值域,与题中的条件作对比,即可得到结论.
解答:由于
 ≠0,∴
≠0,∴ 的值域为{y|y>0,且y≠1},故不满足条件.
的值域为{y|y>0,且y≠1},故不满足条件.由于y=x2+x+1=
 +
+ ≥
≥ ,故值域为[
,故值域为[ ,+∞),故不满足条件.
,+∞),故不满足条件.由于 2x>0,∴
 ≤1,且
≤1,且  ≥0,故函数的值域为[0,1],故不满足条件.
≥0,故函数的值域为[0,1],故不满足条件.由于 2x>0,∴
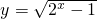 ≥0,故此函数的值域为[0,+∞),故满足条件,
≥0,故此函数的值域为[0,+∞),故满足条件,故选D.
点评:本题主要考查二次函数、指数函数的定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,值域为(0,+∞)的是( )
A、y=(
| ||
B、y=
| ||
C、y=
| ||
D、y=2
|