题目内容
(满分15分)已知椭圆 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为
(1)求椭圆的方程
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C D两点 问:是否存在k的值,使以CD为直径的圆过E点?请说明理由

【答案】
(1) ;(2)存在
;(2)存在 ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.
【解析】第一问中利用A(0,-b)和B(a,0)的坐标,设出直线方程,然后利用椭圆的性质得到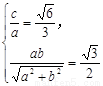
然后求解得到a,b的值。从而得到椭圆方程
第二问中,联立方程组,直线与椭圆联立得到关于x的一元二次方程,利用韦达定理,以及以CD为直径的圆过E点,即当且仅当CE⊥DE时,可知k的值。
解:(1)直线AB方程为:bx-ay-ab=0 依题意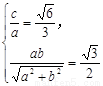 解得
解得 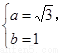
∴ 椭圆方程为  ………………6分
………………6分
(2)假若存在这样的k值,由 得
得
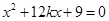
∴  ①
①
设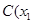 ,
,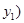
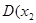 ,
,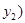 ,则
,则 ②
②
而 ………………10分
………………10分
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则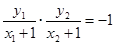 ,即
,即 ∴
∴ 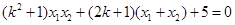 ③
③
将②式代入③整理解得 经验证,
经验证,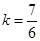 ,使①成立
,使①成立
综上可知,存在 ,使得以CD为直径的圆过点E ………………15分
,使得以CD为直径的圆过点E ………………15分

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 圆
圆