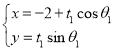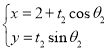题目内容
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,点
,点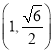 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
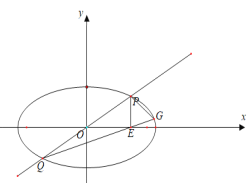
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,![]() 轴,垂足为E,连结QE并延长交C于点G.
轴,垂足为E,连结QE并延长交C于点G.
①求证:![]() 是直角三角形;
是直角三角形;
②求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]()
【解析】
(1)解方程组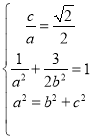 即可;
即可;
(2)①设直线PQ的斜率为k.则其方程为![]() ,联立直线与椭圆方程得到
,联立直线与椭圆方程得到![]() 坐标,再由QG与椭圆方程联立得到G点坐标,证明斜率乘积等于
坐标,再由QG与椭圆方程联立得到G点坐标,证明斜率乘积等于![]() 即可;②利用两点间的距离公式算得
即可;②利用两点间的距离公式算得![]() 的长度,将三角形的面积用k表示,再结合双勾函数的单调性即可得到答案.
的长度,将三角形的面积用k表示,再结合双勾函数的单调性即可得到答案.
(1)由题意,![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,
所以椭圆的方程为:![]() .
.
(2)①:设直线PQ的斜率为k.则其方程为![]() .
.
由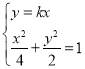 ,得
,得![]() .
.
记![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
于是直线QG的斜率为![]() ,方程为
,方程为![]() .
.
由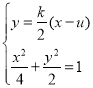 得
得![]() .①
.①
设![]() ,则
,则![]() 和
和![]() 是方程①的解,
是方程①的解,
故![]() ,由此得
,由此得![]() .
.
从而直线PG的斜率为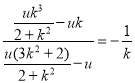 .
.
所以![]() ,即
,即![]() 是直角三角形.
是直角三角形.
②:由①得![]() ,
,![]() ,
,
所以![]() 的面积
的面积![]()
![]()
![]()
![]() ,
,
又![]() ,所以
,所以![]()
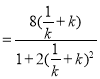 .
.
设![]() ,则由
,则由![]() 得
得![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
因为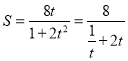 ,而
,而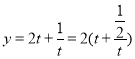 在
在![]() 单调递增,
单调递增,
所以当![]() ,即
,即![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
因此,![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目