题目内容
已知各项均为非负实数的数列{an},{bn}满足:对任意正整数n,都有an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,且a1=0,b1=1.
(I)求证:数列{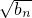 }是等差数列;
}是等差数列;
(II) 设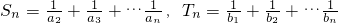 ,当n≥2,n∈N时,试比较
,当n≥2,n∈N时,试比较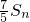 与Tn的大小.
与Tn的大小.
解:(I)∵an,bn,an+1成等差数列,
∴2bn=an+an+1,①
∵bn,an+1,bn+1成等比数列,
∴ ,②
,②
由②得 ,③
,③
将③代入①,得对任意n≥2,n∈N*,
有2bn= ,
,
即2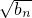 =
= +
+ ,
,
∴{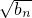 }是等差数列.
}是等差数列.
(II)∵a1=0,b1=1,
∴a2=2,b2=4,a3=6,b3=9,
又{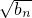 }是等差数列,
}是等差数列,
故 ,
,
当n≥2时,an=n(n-1),
又a1=0,∴an=n(n-1),
∴ ,(n≥2),
,(n≥2),
当n=2时, ,
,
当n=3时, ,
,
当n≥4时, =
= >
> ,
,
而 ,
,
综上,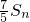 <Tn.
<Tn.
分析:(I)由已知,得2bn=an+an+1, ,故
,故 ,所以2bn=
,所以2bn= ,由此能够证明{
,由此能够证明{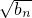 }是等差数列.
}是等差数列.
(II)由a1=0,b1=1,得a2=2,b2=4,a3=6,b3=9,由{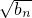 }是等差数列,得
}是等差数列,得 ,由此入手能够证明
,由此入手能够证明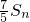 <Tn.
<Tn.
点评:本题考查等差数列的证明和不等式的证明,综合性强,难度大,是高考的重点.解题时要认真审题,熟练掌握等差数列、等比数列的通项公式和前n项和公式的灵活运用.
∴2bn=an+an+1,①
∵bn,an+1,bn+1成等比数列,
∴
 ,②
,②由②得
 ,③
,③将③代入①,得对任意n≥2,n∈N*,
有2bn=
 ,
,即2
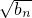 =
= +
+ ,
,∴{
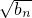 }是等差数列.
}是等差数列.(II)∵a1=0,b1=1,
∴a2=2,b2=4,a3=6,b3=9,
又{
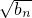 }是等差数列,
}是等差数列,故
 ,
,当n≥2时,an=n(n-1),
又a1=0,∴an=n(n-1),
∴
 ,(n≥2),
,(n≥2),当n=2时,
 ,
,当n=3时,
 ,
,当n≥4时,
 =
= >
> ,
,而
 ,
,综上,
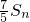 <Tn.
<Tn.分析:(I)由已知,得2bn=an+an+1,
 ,故
,故 ,所以2bn=
,所以2bn= ,由此能够证明{
,由此能够证明{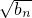 }是等差数列.
}是等差数列.(II)由a1=0,b1=1,得a2=2,b2=4,a3=6,b3=9,由{
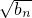 }是等差数列,得
}是等差数列,得 ,由此入手能够证明
,由此入手能够证明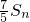 <Tn.
<Tn.点评:本题考查等差数列的证明和不等式的证明,综合性强,难度大,是高考的重点.解题时要认真审题,熟练掌握等差数列、等比数列的通项公式和前n项和公式的灵活运用.

练习册系列答案
相关题目
 }是等差数列;
}是等差数列;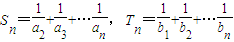 ,当n≥2,n∈N时,试比较
,当n≥2,n∈N时,试比较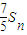 与Tn的大小.
与Tn的大小.