题目内容
若当a∈(0,1)时,由x、y满足的关系式logax+3logxa-logxy=3确定的函数y=f(x)的最大值为
,求a的值及y最大时相应的x的值.
| ||
| 4 |
分析:把原方程转化为logax+
-
=3,即logay=loga2x-3logax+3=(logax-
)2+
,然后利用二次函数的性质求如果y有最大值
时a和x的值.
| 3 |
| logax |
| logay |
| logax |
| 3 |
| 2 |
| 3 |
| 4 |
| ||
| 4 |
解答:解:由所给关系式变形为:logay=(logax-
)2+
…(3分)
∵y=f(x)有最大值
,且0<a<1,∴logay有最小值loga
…(6分)
当logax=
时,loga
=
…(8分)
∴a=
…(10分)
此时log
x=
∴x=
即a=
,x=
为所求…(12分)
| 3 |
| 2 |
| 3 |
| 4 |
∵y=f(x)有最大值
| ||
| 4 |
| ||
| 4 |
当logax=
| 3 |
| 2 |
| ||
| 4 |
| 3 |
| 4 |
∴a=
| 1 |
| 4 |
此时log
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 8 |
即a=
| 1 |
| 4 |
| 1 |
| 8 |
点评:本小题主要考查函数单调性的应用、对数函数的值域与最值、对数方程式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 ,求a的值及y最大时相应的x的值.
,求a的值及y最大时相应的x的值.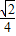 ,求a的值及y最大时相应的x的值.
,求a的值及y最大时相应的x的值.