题目内容
已知实数k满足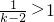 .则方程x2-kx+1=0的两个根可分别作为
.则方程x2-kx+1=0的两个根可分别作为
- A.一椭圆和一双曲线的离心率
- B.两抛物线的离心率
- C.一椭圆和一抛物线的离心率
- D.两椭圆的离心率
A
分析:由题意求出k的范围,判断方程的两个根的范围,即可判断正确选项.
解答:因为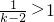 ,解得:2<k<3,方程x2-kx+1=0,可知k2-4>0,
,解得:2<k<3,方程x2-kx+1=0,可知k2-4>0,
当x=1时,x2-kx+1<0,x=0时x2-kx+1>0,所以方程的根一个大于1,一个在(0,1)之间.
所以方程x2-kx+1=0的两个根可分别作为一椭圆和一双曲线的离心率.
故选A.
点评:本题是基础题,考查不等式的解法,函数的零点与方程的根,二次曲线的判断,考查计算能力.
分析:由题意求出k的范围,判断方程的两个根的范围,即可判断正确选项.
解答:因为
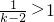 ,解得:2<k<3,方程x2-kx+1=0,可知k2-4>0,
,解得:2<k<3,方程x2-kx+1=0,可知k2-4>0,当x=1时,x2-kx+1<0,x=0时x2-kx+1>0,所以方程的根一个大于1,一个在(0,1)之间.
所以方程x2-kx+1=0的两个根可分别作为一椭圆和一双曲线的离心率.
故选A.
点评:本题是基础题,考查不等式的解法,函数的零点与方程的根,二次曲线的判断,考查计算能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
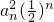 的前n项和.
的前n项和. 的前n项和.
的前n项和.