题目内容
若数列{an}满足an+12-an2=d,其中d为常数,则称数列{an}为等方差数列.已知等方差数列{an}满足an>0,a1=1,a5=3.
(1)求数列{an}的通项公式.
(2)求数列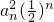 的前n项和.
的前n项和.
(3)记bn=nan2,则当实数k大于4时,不等式kbn大于n(4-k)+4能否对于一切的n∈N*恒成立?请说明理由.
解:(1)由a1=1,a5=3得,
a52-a12=4d,
∴d=2.
∴an2=1+(n-1)×2=2n-1
∵an>0,
∴an= ,
,
数列{an}的通项公式为an= ;
;
(2) =(2n-1)
=(2n-1) ,
,
设Sn=1• +3•
+3• +5•
+5• +…+(2n-1)•
+…+(2n-1)• ①
①
 Sn=1•
Sn=1• +3•
+3• +5•
+5• +…+(2n-1)•
+…+(2n-1)• ②
②
①-②,得
∴ Sn=
Sn= +2(
+2( +
+ +…+
+…+ )-(2n-1)•
)-(2n-1)•
= +
+ -(2n-1)•
-(2n-1)•
∴Sn=3- .
.
即数列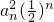 的前n项和为3-
的前n项和为3- ;
;
(3)解法一:bn=n(2n-1),不等式kbn>n(4-k)+4恒成立,
即kn2-2n-2>0对于一切的n∈N+恒成立.
设g(n)=kn2-2n-2.
当k>时,由于对称轴n= <1,且g(1)=k-2-2>0
<1,且g(1)=k-2-2>0
而函数g(n)在[1,+∞)是增函数,
∴不等式kbn>n(4-k)+4恒成立,
即当k>4时,不等式kbn>n(4-k)+4对于一切的n∈N+恒成立.
解法二:bn=n(2n-1),不等式kbn>n(4-k)+4恒成立,即kn2-2n-2>0对于一切的n∈N+恒成立.
∴k>
∴n≥1,∴ ≤4.
≤4.
而k>4
∴k> 恒成立.
恒成立.
故当k>4时,不等式kbn>n(4-k)+4对于一切的n∈N+恒成立.
分析:(1)要求数列的通项公式,我们根据数列{an}为等方差数列,且a1=1,a5=3.我们根据等方差数列的定义:an+12-an2=d我们可以构造一个关于d的方程,解方程求出公差d,进而求出数列的通项公式.
(2)由(1)的结论我们易给出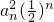 的通项公式,然后利用错位相消法,即可求出数列
的通项公式,然后利用错位相消法,即可求出数列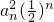 的前n项和.
的前n项和.
(3)要证明当实数k大于4时,不等式kbn大于n(4-k)+4对于一切的n∈N*恒成立,我们有两种思路:一是由bn=nan2,给出数列bn的通项公式,然后构造函数g(n)=kn2-2n-2,通过证明函数g(n)=kn2-2n-2的单调性进行证明;二是转化为证明k> ,即k大于
,即k大于 的最大值恒成立.
的最大值恒成立.
点评:如果一个数列的各项是由一个等差数列与一个等比数列的对应项的乘积组成,则求此数列的前n项和Sn,一般用乘以其公比然后再添加不可缺少的式子错位相减法,要注意对字母的讨论.
a52-a12=4d,
∴d=2.
∴an2=1+(n-1)×2=2n-1
∵an>0,
∴an=
 ,
,数列{an}的通项公式为an=
 ;
;(2)
 =(2n-1)
=(2n-1) ,
,设Sn=1•
 +3•
+3• +5•
+5• +…+(2n-1)•
+…+(2n-1)• ①
① Sn=1•
Sn=1• +3•
+3• +5•
+5• +…+(2n-1)•
+…+(2n-1)• ②
②①-②,得
∴
 Sn=
Sn= +2(
+2( +
+ +…+
+…+ )-(2n-1)•
)-(2n-1)•
=
 +
+ -(2n-1)•
-(2n-1)•
∴Sn=3-
 .
.即数列
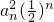 的前n项和为3-
的前n项和为3- ;
;(3)解法一:bn=n(2n-1),不等式kbn>n(4-k)+4恒成立,
即kn2-2n-2>0对于一切的n∈N+恒成立.
设g(n)=kn2-2n-2.
当k>时,由于对称轴n=
 <1,且g(1)=k-2-2>0
<1,且g(1)=k-2-2>0而函数g(n)在[1,+∞)是增函数,
∴不等式kbn>n(4-k)+4恒成立,
即当k>4时,不等式kbn>n(4-k)+4对于一切的n∈N+恒成立.
解法二:bn=n(2n-1),不等式kbn>n(4-k)+4恒成立,即kn2-2n-2>0对于一切的n∈N+恒成立.
∴k>

∴n≥1,∴
 ≤4.
≤4.而k>4
∴k>
 恒成立.
恒成立.故当k>4时,不等式kbn>n(4-k)+4对于一切的n∈N+恒成立.
分析:(1)要求数列的通项公式,我们根据数列{an}为等方差数列,且a1=1,a5=3.我们根据等方差数列的定义:an+12-an2=d我们可以构造一个关于d的方程,解方程求出公差d,进而求出数列的通项公式.
(2)由(1)的结论我们易给出
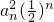 的通项公式,然后利用错位相消法,即可求出数列
的通项公式,然后利用错位相消法,即可求出数列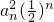 的前n项和.
的前n项和.(3)要证明当实数k大于4时,不等式kbn大于n(4-k)+4对于一切的n∈N*恒成立,我们有两种思路:一是由bn=nan2,给出数列bn的通项公式,然后构造函数g(n)=kn2-2n-2,通过证明函数g(n)=kn2-2n-2的单调性进行证明;二是转化为证明k>
 ,即k大于
,即k大于 的最大值恒成立.
的最大值恒成立.点评:如果一个数列的各项是由一个等差数列与一个等比数列的对应项的乘积组成,则求此数列的前n项和Sn,一般用乘以其公比然后再添加不可缺少的式子错位相减法,要注意对字母的讨论.

练习册系列答案
相关题目
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )

 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
