题目内容
无穷数列1,3,6,10……的通项公式为( )
| A.an=n2-n+1 | B.an=n2+n-1 |
C.an= | D.an= |
C
解析试题分析:法一:(排除法):分别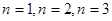 可排除A,B,D,所以选C.
可排除A,B,D,所以选C.
法二:(累加法):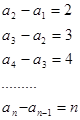
分别相加可得
考点:数列的通项公式

练习册系列答案
相关题目
已知数列 中,
中, ,2
,2 =
=
 ,则数列
,则数列 的通项公式为( )
的通项公式为( )
A. | B. | C. | D. |
已知数列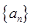 的前n项和为
的前n项和为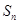 ,且
,且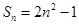 ,则
,则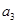 等于( )
等于( )
| A.-10 | B.6 | C.10 | D.14 |
已知数列 的通项公式为
的通项公式为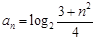 ,那么
,那么 是这个数列的( )
是这个数列的( )
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
若数列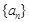 满足:存在正整数
满足:存在正整数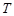 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列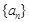 为周期数列,周期为
为周期数列,周期为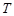 . 已知数列
. 已知数列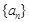 满足
满足 ,
,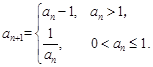
则下列结论中错误的是( )
A.若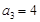 ,则 ,则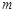 可以取3个不同的值 可以取3个不同的值 |
B.若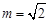 ,则数列 ,则数列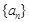 是周期为 是周期为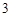 的数列 的数列 |
C. 且 且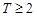 ,存在 ,存在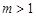 , ,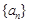 是周期为 是周期为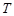 的数列 的数列 |
D.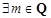 且 且 ,数列 ,数列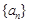 是周期数列 是周期数列 |
已知数列 满足:
满足: ,
, ,且
,且
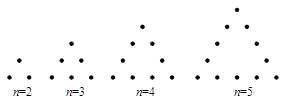
 ,则右图中第9行所有数的和为 ( )
,则右图中第9行所有数的和为 ( ) 
| A.90 | B.9! | C.1022 | D.1024 |
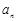 ,则
,则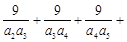 …
…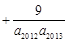 =
= 
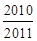
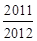
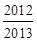
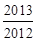
 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列 的前
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )



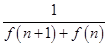 ,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )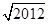 -1
-1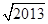 -1
-1 -1
-1