题目内容
随着工业化的发展，环境污染愈来愈严重.某市环保部门随机抽取60名市民对本市空气质量满意度打分，把数据分
、
、
、
六段后得到如下频率分布表：
|
分组 |
频数 |
频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（1）求表中数据
、
、
的值；
（2）用分层抽样的方法在分数
的市民中抽取容量为
的样本，将该样本看成一个总体，从中任取
人在分数段
的概率.
（1）
，
，
；（2）
.
【解析】
试题分析：（1）利用各组数据的概率之和为
求出
的值，然后根据样本容量、总容量以及频率三者之间的关系求出
和
的值；（2）先对所选取的人进行编号，然后将时间空间中的基本事件进行列举，并将事件“分层抽样的方法在分数[60,80）的市民中抽取容量为6的样本，从中任取1人在分数段
”，并确定相应的基本事件数目，然后再利用古典概型的概率计算公式计算相应事件的概率.
试题解析：（1）
，
，
；
（2）∵[60，70）共9人，[70,80)共18人.
∴分层所抽取的6人中[60，70）的2人，[70,80)的4人，分别编号a,b,1,2,3,4设事件A为“从中任取2人，至多有1人在分数段
”。
∵从6人中任取两人的基本事件有15种：（ab）（a1）（a2）（a3）（a4）（b1）（b2）（b3）（b4）（12）（13）（14）（23）（24）（34）
至多有1人在分数段的基本事件有9种：（ab）（a1）（a2）（a3）（a4）（b1）（b2）（b3）（b4）
∴
考点：1.样本容量、总容量以及频率三者之间的关系;2.古典概型
名校课堂系列答案随着经济的发展，人们生活水平的提高，中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况，得右表：
|
|
偏瘦 |
正常 |
肥胖 |
|
女生（人） |
300 |
865 |
|
|
男生（人） |
|
885 |
|
已知从这批学生中随机抽取1名学生，抽到偏瘦男生的概率为0.15.
（Ⅰ）求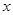
的值；
（Ⅱ）若用分层抽样的方法，从这批学生中随机抽取60名，问应在肥胖学生中抽出多少名？
（Ⅲ）已知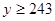
，
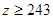，求肥胖学生中男生不少于女生的概率.