题目内容
{an}是由非负整数组成的数列,满足a1=0,a2=3,an+1an=(an-1+2)(an-2+2),n=3,4,5,…,求a3.
解:由已知a4a3=(a2+2)(a1+2)=5×2=10×1,?
∴a3可能取值1,2,5,10.?
若a3=1,a4=10,?
从而a5=![]() ,?
,?
显然a5不是非负整数,与题设矛盾.?
若a3=10,则a4=1,?
从而a5=60.?
但再计算a6=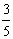 ,也与题设矛盾.?
,也与题设矛盾.?
∴a3=2,a4=5.(或a3=5,a4=2a5![]() N*,舍去)
N*,舍去)
点评:本例用归纳、猜想、证明的思想方法来解决.已给出a1,a2,但递推式是关于连续四项的一个等式,若无其他条件一般是不能确定数列的,因an∈N,我可用整数知识及反证法推理来确定a3=2,a4=5.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
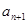 ,
,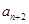 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.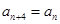 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;