题目内容
已知{an}是由非负整数组成的数列，满足a1=0，a2=3，an=an-2+2，(n∈N*，n≥3)，则数列{an}的通项公式为
an=n+(-1)n
an=n+(-1)n
．分析：易得数列{an}隔项成等差数列，且公差为2，分当n为奇数时，和n为偶数时，写出数列的通项，综合可得答案．
解答：解：由题意可得当n≥3时，an=an-2+2，即an-an-2=2，
故数列{an}隔项成等差数列，且公差为2，
当n为奇数时，an=a1+
d=n-1；
当n为偶数时，an=a2+
d=3+n-2=n+1，
综上可得an=n+(-1)n，
故答案为：an=n+(-1)n
故数列{an}隔项成等差数列，且公差为2，
当n为奇数时，an=a1+
| n-1 |
| 2 |
当n为偶数时，an=a2+
| n-2 |
| 2 |
综上可得an=n+(-1)n，
故答案为：an=n+(-1)n
点评：本题考查等差数列的通项公式，涉及分类讨论的思想，属中档题．
练习册系列答案
相关题目
，
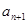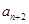…的最小值记为Bn，dn=An－Bn.
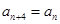)，写出d1，d2，d3，d4的值；