题目内容
已知向量 ,
, ,且
,且 ,则tanx=________.
,则tanx=________.
2
分析:由向量 ,
, ,且
,且 ,知
,知 =sinx-2cosx=0,由此能求出tanx=
=sinx-2cosx=0,由此能求出tanx=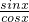 =
= =2.
=2.
解答:∵向量 ,
, ,
,
且 ,
,
∴ =sinx-2cosx=0,
=sinx-2cosx=0,
∴tanx=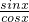 =
= =2.
=2.
故答案为:2.
点评:本题考查平面向量的数量积的计算,解题时要认真审题,注意两个平面向量互相垂直的条件的灵活运用.
分析:由向量
 ,
, ,且
,且 ,知
,知 =sinx-2cosx=0,由此能求出tanx=
=sinx-2cosx=0,由此能求出tanx=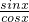 =
= =2.
=2.解答:∵向量
 ,
, ,
,且
 ,
,∴
 =sinx-2cosx=0,
=sinx-2cosx=0,∴tanx=
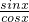 =
= =2.
=2.故答案为:2.
点评:本题考查平面向量的数量积的计算,解题时要认真审题,注意两个平面向量互相垂直的条件的灵活运用.

练习册系列答案
相关题目
已知向量
=(1,m),
=(2,n),
=(3,t),且
∥
,
⊥
,则|
|2+|
|2的最小值为( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、20 | B、16 | C、10 | D、4 |