题目内容
数列![]() 中
中![]() =1,前n项的和
=1,前n项的和![]() 满足关系式
满足关系式![]() (t>0,n=2,3,4,…)
(t>0,n=2,3,4,…)
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的公比为f(t),作数列
的公比为f(t),作数列![]() ,使
,使![]() =1,
=1,![]() ,求和:
,求和:
![]()
(3)在(2)的条件下,求证: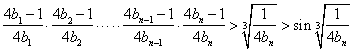
(1)![]() 又
又![]()
相减得:![]() 所以
所以![]() (
(![]() )————3分
)————3分
又![]()
{![]() }为等比数列,公比为
}为等比数列,公比为![]() ——————————————4分
——————————————4分
(2)![]() ——————————————6分
——————————————6分
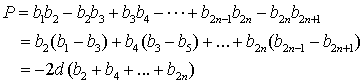
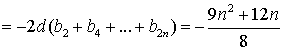 ————————9分
————————9分
(3)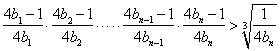 即
即![]()
(法一数学归纳法)当![]() 左边=
左边=![]() =右边
=右边
假设![]() 不等式成立,
不等式成立,
则![]() 时,
时,![]()
![]()
所以![]() 时,不等式成立
时,不等式成立
综上所述,不等式对任意的n均成立 ———————————12分
(法二放缩法)记![]()
![]()
![]()
因为![]() 所以
所以![]()
则![]() ————————12分
————————12分
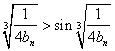 即
即![]() ,而
,而![]()
设 ![]() ,
,![]()
则![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 即
即![]()
所以![]() ————————————————————15分
————————————————————15分

练习册系列答案
相关题目