题目内容
函数f(x)=ax2+bx+c,若x1≠x2时,f(x1)=f(x2),且f(2x1)=f(2x2),则f(2012x1)-f(2012x2)的取值( )A.一定大于零
B.一定等于零
C.一定小于零
D.不能确定正负
【答案】分析:由f(x)=ax2+bx+c,若x1≠x2时,f(x1)=f(x2),且f(2x1)=f(2x2),知x1+x2=0,b=0.所以f(x)=ax2+c,
故f(2012x1)-f(2012x2)=0.
解答:解:∵f(x)=ax2+bx+c,若x1≠x2时,
f(x1)=f(x2),且f(2x1)=f(2x2),
∴抛物线的对称轴x=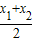 =x1+x2=-
=x1+x2=-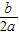 ,
,
∴x1+x2=0,b=0.
∴f(x)=ax2+c,
∴f(2012x1)-f(2012x2)=0.
故选B.
点评:本题考查二次函数的性质的应用,是基础题.解题时要认真审题,仔细解答.
故f(2012x1)-f(2012x2)=0.
解答:解:∵f(x)=ax2+bx+c,若x1≠x2时,
f(x1)=f(x2),且f(2x1)=f(2x2),
∴抛物线的对称轴x=
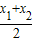 =x1+x2=-
=x1+x2=-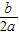 ,
,∴x1+x2=0,b=0.
∴f(x)=ax2+c,
∴f(2012x1)-f(2012x2)=0.
故选B.
点评:本题考查二次函数的性质的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目