题目内容
已知函数
（Ⅰ）将函数f（x）化简成Asin（ωx+φ）+B（A＞0，φ＞0，φ∈[0，2π））的形式，并指出f（x）的周期；
（Ⅱ）求函数
上的最大值和最小值
解：（Ⅰ）
．
故f（x）的周期为2kπ{k∈Z且k≠0}．
（Ⅱ）由π≤x≤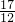
π，得
．
因为f（x）=
在[
]上是减函数，
在[
]上是增函数．
故当x=
时，f（x）有最小值-
；
而f（π）=-2，f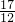（π）=-
＜-2，
所以当x=π时，f（x）有最大值-2．
分析：（Ⅰ）根据题意，化简为Asin（ωx+φ）+B的形式，然后求出f（x）的周期
（Ⅱ）根据题意，求出上的单调区间，然后根据单调性的意义分别求出最大值和最小值．
点评：本题考查Asin（ωx+φ）+B中参数的物理意义，以及三角函数的周期性，还有三角函数的最值．通过求f（x）在已知区间上的单调性来求最值．属于基础题．
．故f（x）的周期为2kπ{k∈Z且k≠0}．
（Ⅱ）由π≤x≤
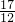π，得．因为f（x）=
在[]上是减函数，在[
]上是增函数．故当x=
时，f（x）有最小值-；而f（π）=-2，f（
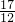π）=-＜-2，所以当x=π时，f（x）有最大值-2．
分析：（Ⅰ）根据题意，
化简为Asin（ωx+φ）+B的形式，然后求出f（x）的周期（Ⅱ）根据题意，求出
上的单调区间，然后根据单调性的意义分别求出最大值和最小值．点评：本题考查Asin（ωx+φ）+B中参数的物理意义，以及三角函数的周期性，还有三角函数的最值．通过求f（x）在已知区间上的单调性来求最值．属于基础题．
练习册系列答案
相关题目
已知函数f（x）=|x-1|+|x+1|（x∈R）
已知函数f（x）=log3（ax+b）的部分图象如图所示．