题目内容
若
对一切x＞0恒成立，则a的取值范围是 ．
【答案】分析：
转化为函数y=|x-a|与y=
，通过函数的图象，即可求出a的取值范围．
解答：
解：
转化为函数y=|x-a|与y=
，
由函数的图象，y=
＜
，且x=2时y=0，
可知a的取值范围是（-∞，2]
故答案为：（-∞，2]
点评：本题主要考查不等式恒成立问题，这类题目往往转化为最值问题解决，还考查了基本不等式及转化思想，分类讨论等思想方法，数形结合的方法．
转化为函数y=|x-a|与y=，通过函数的图象，即可求出a的取值范围．解答：
解：转化为函数y=|x-a|与y=，由函数的图象，y=
＜，且x=2时y=0，可知a的取值范围是（-∞，2]
故答案为：（-∞，2]
点评：本题主要考查不等式恒成立问题，这类题目往往转化为最值问题解决，还考查了基本不等式及转化思想，分类讨论等思想方法，数形结合的方法．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
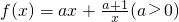，g（x）=4-x，已知满足f（x）=g（x）的x有且只有一个．
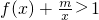对一切x＞0恒成立，求m的取值范围；
对一切x＞0恒成立，则a的取值范围是 ．
对一切x＞0恒成立，则a的取值范围是 ．
对一切x＞0恒成立，则a的取值范围是 ．