题目内容
已知数列{an},{bn}满足:a1=3b1=3,a2=6,bn+1=2bn-2n,bn=an-nan-1(n≥2,n∈N*).
(I)探究数列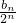 是等差数列还是等比数列,并由此求数列{bn}的通项公式;
是等差数列还是等比数列,并由此求数列{bn}的通项公式;
(II)求数列{nan}的前n项和Sn.
解:(I)∵bn+1=2bn-2n ,∴bn+1-2bn =-2n ,∴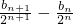 =-
=- .
.
∴数列{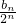 }构成以
}构成以 为首项,以-
为首项,以- 为公差的等差数列,∴
为公差的等差数列,∴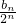 =
= -
- (n-1),
(n-1),
∴bn= ).
).
(II)∵bn=an-nan-1,∴an-2n=nan-1-n2n-1=n( an-1-2n-1 ),
∴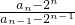 =n,
=n,
∴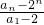 =
=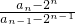 •
•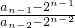 •
•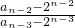 …
…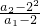
=n(n-1)(n-2)×…×3×2,又 a1=3,故 an=n(n-1)(n-2)×…×3×2×1+2n,
nan=n×n(n-1)(n-2)×…×3×2×1+n 2n=(n+1)!-n!+n 2n,
∴sn=(2!-1!)+(3!-2!)+(4!-3!)+…+((n+1)!-n!)+(1×2+2×22+…+n2n )
=(n+1)!-1+( 1×2+2×22+…+n2n ).
令Tn=1×2+2×22+…+n2n,①则 2Tn=1×22+2×23+…+n 2n+1,②
①-②可得,-Tn=2+22+23+…-n 2n+1,∴Tn=(n-1)2n+1+2,
∴sn=(n+1)!+(n-1)2n+1+1.
分析:(I)由条件可得 数列{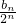 }构成以
}构成以 为首项,以-
为首项,以- 为公差的等差数列,故
为公差的等差数列,故 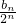 =
= -
- (n-1),从而得到bn.
(n-1),从而得到bn.
(II)先推出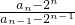 =n,可得
=n,可得 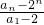 ═n(n-1)(n-2)×…×3×2,得到nan=(n+1)!-n!+n 2n,进而得到 sn=(n+1)!-1+( 1×2+2×22+…+n2n ).用错位相减法求得1×2+2×22+…+n2n 的值,即可得到sn的值.
═n(n-1)(n-2)×…×3×2,得到nan=(n+1)!-n!+n 2n,进而得到 sn=(n+1)!-1+( 1×2+2×22+…+n2n ).用错位相减法求得1×2+2×22+…+n2n 的值,即可得到sn的值.
点评:本题考查等差数列、等比数列的定义、性质,以及求和公式的应用,用错位相减法进行数列求和,得到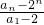 =
=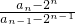 •
•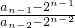 •
•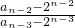 …
…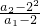 ,是解题的难点.
,是解题的难点.
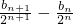 =-
=- .
.∴数列{
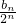 }构成以
}构成以 为首项,以-
为首项,以- 为公差的等差数列,∴
为公差的等差数列,∴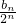 =
= -
- (n-1),
(n-1),∴bn=
 ).
).(II)∵bn=an-nan-1,∴an-2n=nan-1-n2n-1=n( an-1-2n-1 ),
∴
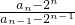 =n,
=n,∴
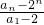 =
=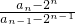 •
•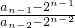 •
•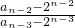 …
…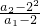
=n(n-1)(n-2)×…×3×2,又 a1=3,故 an=n(n-1)(n-2)×…×3×2×1+2n,
nan=n×n(n-1)(n-2)×…×3×2×1+n 2n=(n+1)!-n!+n 2n,
∴sn=(2!-1!)+(3!-2!)+(4!-3!)+…+((n+1)!-n!)+(1×2+2×22+…+n2n )
=(n+1)!-1+( 1×2+2×22+…+n2n ).
令Tn=1×2+2×22+…+n2n,①则 2Tn=1×22+2×23+…+n 2n+1,②
①-②可得,-Tn=2+22+23+…-n 2n+1,∴Tn=(n-1)2n+1+2,
∴sn=(n+1)!+(n-1)2n+1+1.
分析:(I)由条件可得 数列{
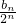 }构成以
}构成以 为首项,以-
为首项,以- 为公差的等差数列,故
为公差的等差数列,故 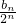 =
= -
- (n-1),从而得到bn.
(n-1),从而得到bn.(II)先推出
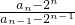 =n,可得
=n,可得 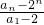 ═n(n-1)(n-2)×…×3×2,得到nan=(n+1)!-n!+n 2n,进而得到 sn=(n+1)!-1+( 1×2+2×22+…+n2n ).用错位相减法求得1×2+2×22+…+n2n 的值,即可得到sn的值.
═n(n-1)(n-2)×…×3×2,得到nan=(n+1)!-n!+n 2n,进而得到 sn=(n+1)!-1+( 1×2+2×22+…+n2n ).用错位相减法求得1×2+2×22+…+n2n 的值,即可得到sn的值.点评:本题考查等差数列、等比数列的定义、性质,以及求和公式的应用,用错位相减法进行数列求和,得到
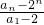 =
=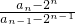 •
•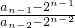 •
•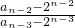 …
…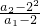 ,是解题的难点.
,是解题的难点. 
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目