题目内容
函数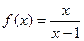
⑴求证: 的图像关于直线y=x对称;
的图像关于直线y=x对称;
⑵函数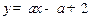 的图像与函数
的图像与函数 的图像有且只有一个交点,求实数
的图像有且只有一个交点,求实数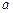 的值;
的值;
⑶是否存在圆心在原点的圆与函数 的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。
的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。
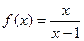
⑴求证:
 的图像关于直线y=x对称;
的图像关于直线y=x对称;⑵函数
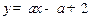 的图像与函数
的图像与函数 的图像有且只有一个交点,求实数
的图像有且只有一个交点,求实数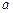 的值;
的值;⑶是否存在圆心在原点的圆与函数
 的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。
的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。(1)见解析(2)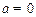 或
或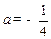 (3)见解析
(3)见解析
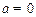 或
或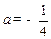 (3)见解析
(3)见解析⑴解一:由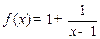 可知函数图像即为反比例函数
可知函数图像即为反比例函数 的图像经向右平移1个单位后再向上平移1个单位得到。则函数图像关于直线y=x对称…………………………………….….4’
的图像经向右平移1个单位后再向上平移1个单位得到。则函数图像关于直线y=x对称…………………………………….….4’
解二:函数 的反函数
的反函数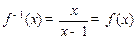 ,所以
,所以 的图像关于直线y=x对称………….4’
的图像关于直线y=x对称………….4’
⑵由题意得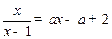 有且只有一解。
有且只有一解。
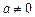 时,由判别式等于0可得
时,由判别式等于0可得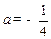 ……………………………………3’
……………………………………3’
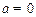 时,由图像易得同样满足题意………………………..………………2’
时,由图像易得同样满足题意………………………..………………2’
所以……………………………………………..………..…1’
⑶解一:由函数图像可得若存在满足题意的圆,则圆与函数 的图像必在第一象限相切,即圆过(2,2)点,可得圆半径为
的图像必在第一象限相切,即圆过(2,2)点,可得圆半径为 ,所以存在满足题意的圆,其半径为
,所以存在满足题意的圆,其半径为 ……....4’
……....4’
r = 代回检验得满足题目要求,所以存在满足题意的圆,其半径为
代回检验得满足题目要求,所以存在满足题意的圆,其半径为 …..2’
…..2’
解二:由⑴与圆的对称性可得交点必关于直线y=x对称 ……………...…..2’
如果有且仅有三个交点,则必有一个交点在直线y=x上,即这个交点就是函数y= 与直线y=x的交点 ……………………………………….……..…..2’
与直线y=x的交点 ……………………………………….……..…..2’
求得交点有两个(0,0)、(2,2),其中(0,0)不满足题意,而过(2,2)时圆的半径为 。r =
。r = 代回检验得满足题目要求,所以存在满足题意的圆,其半径为
代回检验得满足题目要求,所以存在满足题意的圆,其半径为
所以存在满足题意的圆,其半径为 .…………..2’
.…………..2’
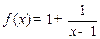 可知函数图像即为反比例函数
可知函数图像即为反比例函数 的图像经向右平移1个单位后再向上平移1个单位得到。则函数图像关于直线y=x对称…………………………………….….4’
的图像经向右平移1个单位后再向上平移1个单位得到。则函数图像关于直线y=x对称…………………………………….….4’解二:函数
 的反函数
的反函数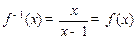 ,所以
,所以 的图像关于直线y=x对称………….4’
的图像关于直线y=x对称………….4’⑵由题意得
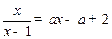 有且只有一解。
有且只有一解。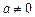 时,由判别式等于0可得
时,由判别式等于0可得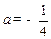 ……………………………………3’
……………………………………3’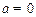 时,由图像易得同样满足题意………………………..………………2’
时,由图像易得同样满足题意………………………..………………2’所以……………………………………………..………..…1’
⑶解一:由函数图像可得若存在满足题意的圆,则圆与函数
 的图像必在第一象限相切,即圆过(2,2)点,可得圆半径为
的图像必在第一象限相切,即圆过(2,2)点,可得圆半径为 ,所以存在满足题意的圆,其半径为
,所以存在满足题意的圆,其半径为 ……....4’
……....4’r =
 代回检验得满足题目要求,所以存在满足题意的圆,其半径为
代回检验得满足题目要求,所以存在满足题意的圆,其半径为 …..2’
…..2’解二:由⑴与圆的对称性可得交点必关于直线y=x对称 ……………...…..2’
如果有且仅有三个交点,则必有一个交点在直线y=x上,即这个交点就是函数y=
 与直线y=x的交点 ……………………………………….……..…..2’
与直线y=x的交点 ……………………………………….……..…..2’求得交点有两个(0,0)、(2,2),其中(0,0)不满足题意,而过(2,2)时圆的半径为
 。r =
。r = 代回检验得满足题目要求,所以存在满足题意的圆,其半径为
代回检验得满足题目要求,所以存在满足题意的圆,其半径为
所以存在满足题意的圆,其半径为
 .…………..2’
.…………..2’
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 (
( 为正实数,
为正实数, )的定义域恰为区间
)的定义域恰为区间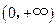 ,是否存在这样的
,是否存在这样的 ,
, 使得:
使得: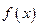 恰在
恰在 上取正值,且
上取正值,且 ?若存在,求出
?若存在,求出 的定义域是 .
的定义域是 . 的图象至多有一个公共点,则实数b的取值范围是__________.
的图象至多有一个公共点,则实数b的取值范围是__________. ,y2=0.5
,y2=0.5 ,则 ( )
,则 ( ) 的解集是 .
的解集是 .