题目内容
一束光线过点 射到x轴上,再反射到圆C:(x-1)2+(y+4)2=8上,
射到x轴上,再反射到圆C:(x-1)2+(y+4)2=8上,(1)当反射光线经过圆心时,求反射光线所在的直线方程的一般式;
(2)求反射点的横坐标的变化范围.
【答案】分析:(1)由题意可得:M点关于x轴的对称点为,由反射光线的反向延长线经过与圆的圆心(1,-4)可得直线的方程.
(2)当反射光线的斜率存在时,设其方程为: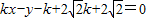 ,当反射光线与圆相切时为反射点的最大范围,由点到直线的距离公式可得k的值,再检验斜率不存在时直线也与圆相切,进而得到答案.
,当反射光线与圆相切时为反射点的最大范围,由点到直线的距离公式可得k的值,再检验斜率不存在时直线也与圆相切,进而得到答案.
解答:解:(1)由题意可得:M点关于x轴的对称点为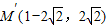 ,
,
因为反射光线的反向延长线经过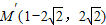 与圆的圆心(1,-4),
与圆的圆心(1,-4),
所以反射光线所在的直线的方程为: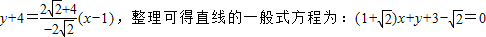 .
.
(2)当反射光线的斜率存在时,设其方程为: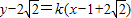 ,
,
整理可得: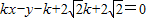 .
.
由题意可得:当反射光线与圆相切时为反射点的最大范围,
所以有圆心到反射光线的距离等于半径,即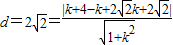 ,
,
解得:k=-1,此时反射光线的方程为x+y-1=0,
所以反射点为(1,0).
当斜率不存在时,经检验也与圆相切,则反射点的横坐标的取值范围是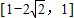 .
.
点评:解决此类问题的关键是熟练掌握直线与圆的位置关系,以及直线方程的一般式与两点式,考查点到直线的距离公式等知识点,此题综合性较强属于中档题.
(2)当反射光线的斜率存在时,设其方程为:
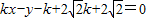 ,当反射光线与圆相切时为反射点的最大范围,由点到直线的距离公式可得k的值,再检验斜率不存在时直线也与圆相切,进而得到答案.
,当反射光线与圆相切时为反射点的最大范围,由点到直线的距离公式可得k的值,再检验斜率不存在时直线也与圆相切,进而得到答案.解答:解:(1)由题意可得:M点关于x轴的对称点为
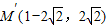 ,
,因为反射光线的反向延长线经过
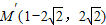 与圆的圆心(1,-4),
与圆的圆心(1,-4),所以反射光线所在的直线的方程为:
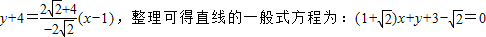 .
.(2)当反射光线的斜率存在时,设其方程为:
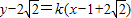 ,
,整理可得:
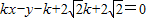 .
.由题意可得:当反射光线与圆相切时为反射点的最大范围,
所以有圆心到反射光线的距离等于半径,即
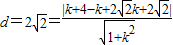 ,
,解得:k=-1,此时反射光线的方程为x+y-1=0,
所以反射点为(1,0).
当斜率不存在时,经检验也与圆相切,则反射点的横坐标的取值范围是
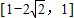 .
.点评:解决此类问题的关键是熟练掌握直线与圆的位置关系,以及直线方程的一般式与两点式,考查点到直线的距离公式等知识点,此题综合性较强属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 射到x轴上,再反射到圆C:
射到x轴上,再反射到圆C: 上,
上,